
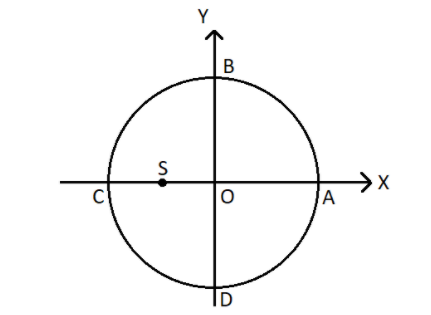
A small object moves counter clockwise along the circular path whose centre is at origin as shown in figure. As it moves along the path, its acceleration vector continuously points towards point S. Then the object
(A) Speed up as it moves from A to C via B.
(B) Slow down as it moves from A to C via B.
(C) Slow down as it moves from C to A via D.
(D) Speed up as it moves from C to A via D.
Answer
180k+ views
Hint: When an object moves in a circular path its tangential velocity always changes. It is to be remembered that velocity is a vector quantity and it has both magnitude and direction.
Formula Used: The formulae used in the solution are given here.
For a dot product of vectors $\vec m$ and $\vec n$, $\vec m \cdot \vec n = \left| m \right|\left| n \right|\cos \theta $ where $\theta $ is the angle between the two vectors $\vec m$ and $\vec n$.
Complete Step by Step Solution: Law of Conservation of Angular Momentum states that, when an object moves around a fixed axis at a variable distance, and no external torque acts on the system, the total angular momentum remains constant.
Uniform circular motion is a specific type of motion in which an object travels in a circle with a constant speed.
It has been given that, a small object moves counter clockwise along the circular path whose centre is at origin and as it moves along the path, its acceleration vector continuously points towards point S.
As we know that, when an object moves in a circular path its tangential velocity always changes. It is to be remembered that velocity is a vector quantity and it has both magnitude and direction.
For a dot product of vectors $\vec m$ and $\vec n$, $\vec m \cdot \vec n = \left| m \right|\left| n \right|\cos \theta $ where $\theta $ is the angle between the two vectors $\vec m$ and $\vec n$.
The product of acceleration and velocity is given by, $\left( {\vec a \cdot \vec v} \right)$. When $\left( {\vec a \cdot \vec v} \right)$ is positive, then the object speeds up and the $\left( {\vec a \cdot \vec v} \right)$ is negative, thus it slows down.
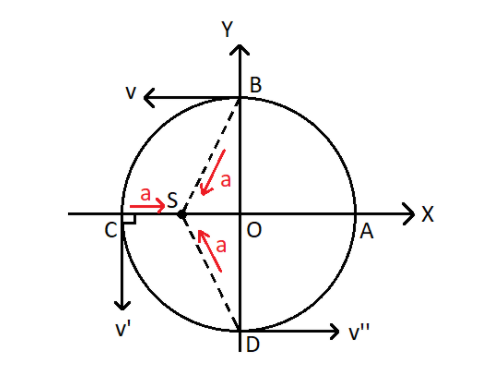
At point B, we have a positive value of $\left( {\vec a \cdot \vec v} \right)$, since $\theta < 90$ which implies that the body speeds up here.
At point D, $\left( {\vec a \cdot \vec v} \right)$ has a negative value, since $\theta > 90$, which implies that the body slows down here.
At point C, $\theta = {90^ \circ }$, we have $\left( {\vec a \cdot \vec v} \right) = 0$.
From the information obtained above, we can say that the object speeds up as it moves from A to C via B.
Hence the correct answer is Option A.
Note: Two vectors are said to equal if their magnitude and direction are the same. According to vector algebra, a vector can be added to another vector, head to tail. The order of addition of two vectors does not matter, because the result will be the same.
The cross product of two vectors results in a vector quantity. It is represented by a cross sign between two vectors. The dot product of two vectors always results in scalar quantity, i.e. it has only magnitude and no direction. It is represented by a dot (.) in between two vectors.
Formula Used: The formulae used in the solution are given here.
For a dot product of vectors $\vec m$ and $\vec n$, $\vec m \cdot \vec n = \left| m \right|\left| n \right|\cos \theta $ where $\theta $ is the angle between the two vectors $\vec m$ and $\vec n$.
Complete Step by Step Solution: Law of Conservation of Angular Momentum states that, when an object moves around a fixed axis at a variable distance, and no external torque acts on the system, the total angular momentum remains constant.
Uniform circular motion is a specific type of motion in which an object travels in a circle with a constant speed.
It has been given that, a small object moves counter clockwise along the circular path whose centre is at origin and as it moves along the path, its acceleration vector continuously points towards point S.
As we know that, when an object moves in a circular path its tangential velocity always changes. It is to be remembered that velocity is a vector quantity and it has both magnitude and direction.
For a dot product of vectors $\vec m$ and $\vec n$, $\vec m \cdot \vec n = \left| m \right|\left| n \right|\cos \theta $ where $\theta $ is the angle between the two vectors $\vec m$ and $\vec n$.
The product of acceleration and velocity is given by, $\left( {\vec a \cdot \vec v} \right)$. When $\left( {\vec a \cdot \vec v} \right)$ is positive, then the object speeds up and the $\left( {\vec a \cdot \vec v} \right)$ is negative, thus it slows down.

At point B, we have a positive value of $\left( {\vec a \cdot \vec v} \right)$, since $\theta < 90$ which implies that the body speeds up here.
At point D, $\left( {\vec a \cdot \vec v} \right)$ has a negative value, since $\theta > 90$, which implies that the body slows down here.
At point C, $\theta = {90^ \circ }$, we have $\left( {\vec a \cdot \vec v} \right) = 0$.
From the information obtained above, we can say that the object speeds up as it moves from A to C via B.
Hence the correct answer is Option A.
Note: Two vectors are said to equal if their magnitude and direction are the same. According to vector algebra, a vector can be added to another vector, head to tail. The order of addition of two vectors does not matter, because the result will be the same.
The cross product of two vectors results in a vector quantity. It is represented by a cross sign between two vectors. The dot product of two vectors always results in scalar quantity, i.e. it has only magnitude and no direction. It is represented by a dot (.) in between two vectors.
Recently Updated Pages
Class 11 JEE Main Physics Mock Test - FREE Online Mock Test Series 2025

Degree of Dissociation Important Concepts and Tips for JEE

Learn Conversion of Galvanometer into Ammeter and Voltmeter for JEE Main

JEE Main Chemistry Question Paper PDF Download with Answer Key

Electric Field Due To Uniformly Charged Ring - JEE Main 2025

JEE Electricity and Magnetism Important Concepts and Tips for Exam Preparation

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

JEE Main 2025: Derivation of Equation of Trajectory in Physics

Displacement-Time Graph and Velocity-Time Graph for JEE

Atomic Structure - Electrons, Protons, Neutrons and Atomic Models

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

What is Hybridisation in Chemistry?

Other Pages
NCERT Solutions For Class 11 Physics Chapter 2 Motion In A Straight Line - 2025-26

NCERT Solutions For Class 11 Physics Chapter 1 Units and Measurements - 2025-26

NCERT Solutions For Class 11 Physics Chapter 3 Motion In A Plane - 2025-26

JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26

Motion in a Straight Line Class 11 Physics Chapter 2 CBSE Notes - 2025-26




