
The system shown is just on the verge of slipping. The coefficient of static friction between the block and the tabletop is
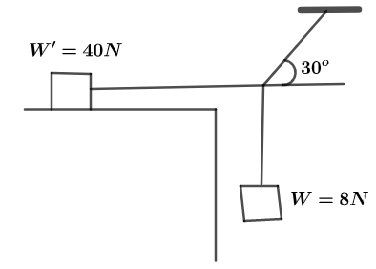
(A) $0.5$
(B) $0.95$
(C) $0.15$
(D) $0.35$
Answer
180k+ views
Hint: In order to solve this question, we will first draw the free diagram with all the forces acting on the blocks and string of the system and then by applying the forces equilibrium condition, we will solve for the coefficient of static friction between the block and tabletop.
Complete answer:
Let us first draw the free diagram of the system with all the forces acting on the system as
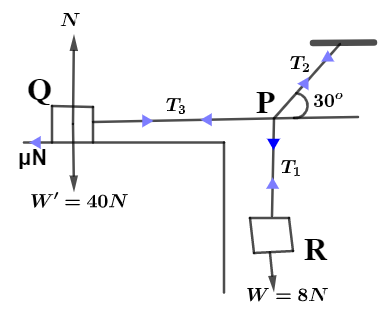
where, N is the normal force for block Q, ${T_1},{T_2},{T_3}$ be the Tension force acting on the strings and $\mu N$ be the static frictional force between block Q and tabletop. Now,
For equilibrium of block R we have,
${T_1} = W = 8N$
Equilibrium at point P, the vertical component of ${T_2}$ is equal to ${T_1}$ so, we have
${T_2}\sin {30^o} = {T_1}$
on putting the values, we get
$
{T_2}\dfrac{1}{2} = 8 \\
{T_2} = 16N \\
$
Now, the horizontal component of ${T_2}$ is equal to ${T_3}$ so, equilibrium for block Q is
${T_2}\cos {30^o} = {T_3}$
on putting the values, we get
$
(16)\dfrac{{\sqrt 3 }}{2} = {T_3} \\
{T_3} = 8\sqrt 3 N \\
$
Now, normal reaction force on block Q is $N = W' = 40N$ and the static frictional force is balanced by the tension ${T_3} = \mu N$
so, on putting the values we get
$
8\sqrt 3 = \mu (40) \\
\mu = \dfrac{{\sqrt 3 }}{5} \\
\mu = 0.35 \\
$
So, the coefficient of static friction between tabletop and block is $\mu = 0.35$
Hence, the correct answer is option (D) $0.35$
Note: It should be remembered that, basic trigonometric values must be known which are used here as
$
\sin {30^o} = \dfrac{1}{2} \\
\cos {30^o} = \dfrac{{\sqrt 3 }}{2} \\
$
And always draw the free diagram with all necessary forces acting on the system with their direction to solve such problems.
Complete answer:
Let us first draw the free diagram of the system with all the forces acting on the system as

where, N is the normal force for block Q, ${T_1},{T_2},{T_3}$ be the Tension force acting on the strings and $\mu N$ be the static frictional force between block Q and tabletop. Now,
For equilibrium of block R we have,
${T_1} = W = 8N$
Equilibrium at point P, the vertical component of ${T_2}$ is equal to ${T_1}$ so, we have
${T_2}\sin {30^o} = {T_1}$
on putting the values, we get
$
{T_2}\dfrac{1}{2} = 8 \\
{T_2} = 16N \\
$
Now, the horizontal component of ${T_2}$ is equal to ${T_3}$ so, equilibrium for block Q is
${T_2}\cos {30^o} = {T_3}$
on putting the values, we get
$
(16)\dfrac{{\sqrt 3 }}{2} = {T_3} \\
{T_3} = 8\sqrt 3 N \\
$
Now, normal reaction force on block Q is $N = W' = 40N$ and the static frictional force is balanced by the tension ${T_3} = \mu N$
so, on putting the values we get
$
8\sqrt 3 = \mu (40) \\
\mu = \dfrac{{\sqrt 3 }}{5} \\
\mu = 0.35 \\
$
So, the coefficient of static friction between tabletop and block is $\mu = 0.35$
Hence, the correct answer is option (D) $0.35$
Note: It should be remembered that, basic trigonometric values must be known which are used here as
$
\sin {30^o} = \dfrac{1}{2} \\
\cos {30^o} = \dfrac{{\sqrt 3 }}{2} \\
$
And always draw the free diagram with all necessary forces acting on the system with their direction to solve such problems.
Recently Updated Pages
Class 11 JEE Main Physics Mock Test - FREE Online Mock Test Series 2025

Degree of Dissociation Important Concepts and Tips for JEE

Learn Conversion of Galvanometer into Ammeter and Voltmeter for JEE Main

JEE Main Chemistry Question Paper PDF Download with Answer Key

Electric Field Due To Uniformly Charged Ring - JEE Main 2025

JEE Electricity and Magnetism Important Concepts and Tips for Exam Preparation

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

JEE Main 2025: Derivation of Equation of Trajectory in Physics

Displacement-Time Graph and Velocity-Time Graph for JEE

Atomic Structure - Electrons, Protons, Neutrons and Atomic Models

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

What is Hybridisation in Chemistry?

Other Pages
NCERT Solutions For Class 11 Physics Chapter 2 Motion In A Straight Line - 2025-26

NCERT Solutions For Class 11 Physics Chapter 1 Units and Measurements - 2025-26

NCERT Solutions For Class 11 Physics Chapter 3 Motion In A Plane - 2025-26

JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26

Motion in a Straight Line Class 11 Physics Chapter 2 CBSE Notes - 2025-26




