




How Does the Division Property of Equality Help You Solve Equations?
Division is a method of distributing evenly and fairly. Similarly, in an equation you need to operate on both sides of the equation fairly. Whatever you operate on the left side of an equation, you must do it on the right side of the equation as well. You cannot divide something from one side without performing anything on the other side.
Suppose, you have two cakes of equal size. And you have 8 guests at the party. You have to divide both the cakes evenly throughout. How will you be able to do this?
To divide both the cakes evenly, you can cut each cake into 4 pieces. If you divide each cake into 4 pieces, you will be left with a total of 8 pieces of cakes. Now you can easily distribute an equal piece of cake among your 8 guests.
In short, cutting both the cakes evenly to get the balance is the division property of equality.
How to Divide an Equation Equally?
The division property of equality states that if you divide both sides of an equation by the same non zero number, the two sides remain equal.
In other words, if a, b, and c are real numbers, such that a = b , and c ≠ 0, then \[\frac{a}{c} = \frac{b}{c} \]
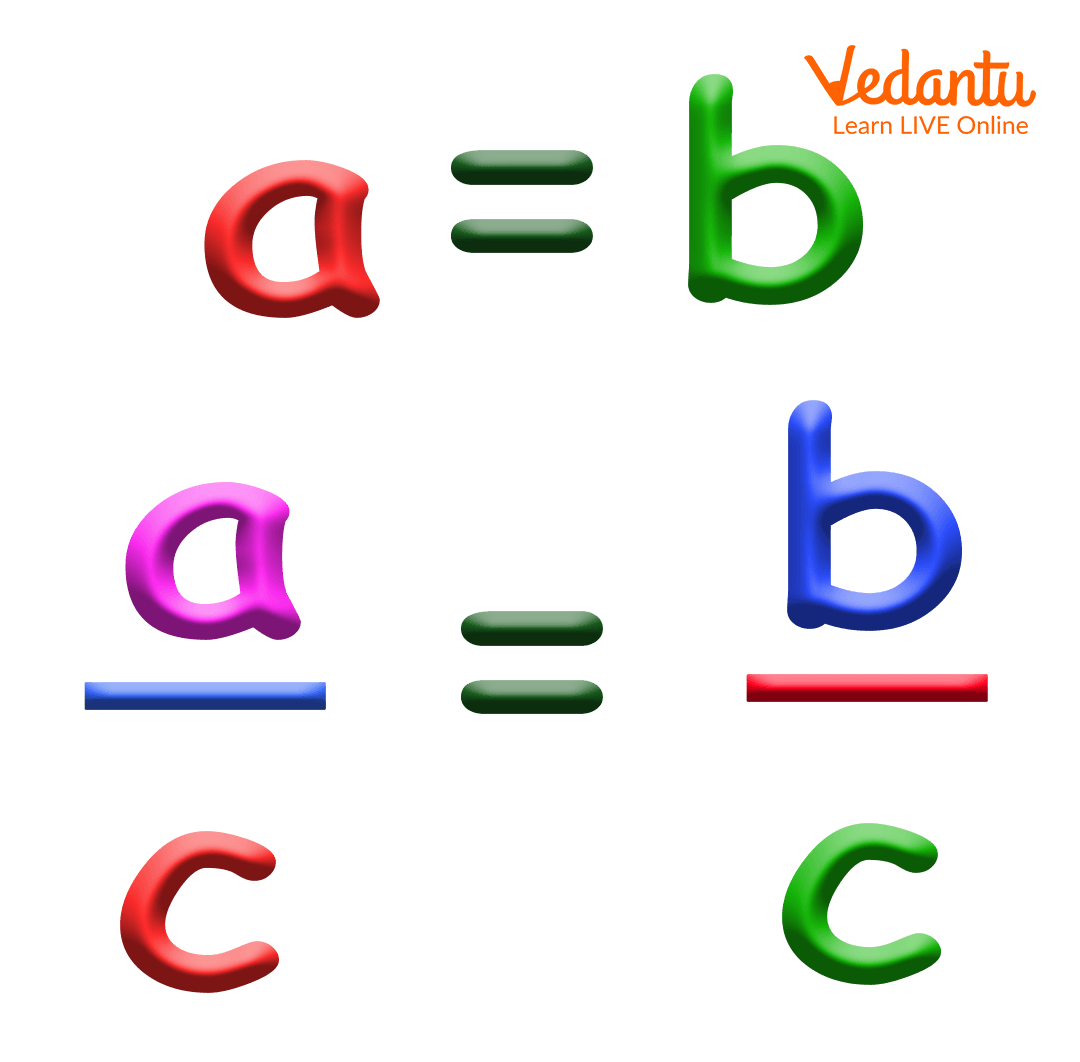
Division Property of Equality
Let us understand with an example:
Consider the equation, 20 = 20
Divide both the sides by 2.
\[\frac{20}{2} = \frac{20}{2} \]
10 = 10
LHS = RHS
The equation remains balanced.
Division Property of Equality Definition
The division property of equality states that dividing both sides of an equation by the same number does not affect the equation.
In other words, it states that if you are given an equation and you divide each side of an equation equally, the equation will always remain balanced and equal. This is termed as division property of equality.
Division Property of Equality Formula
The division property of equality formula states that:
Division Property of Equality Proof
To prove the division property of the equality statement, we will consider the following linear equation.
Consider the equation 5x = 30,
Dividing both sides of the equation by 5:
5x = 30
\[\frac{5x}{5} = \frac{30}{5} \]
x = 6
Therefore, the value of x is 6.
Hence, we applied the division property of equality here to solve for x.
You can verify, if x = 6 is the solution of the given equation by substituting x = 6 in the given equation.
LHS = 5x
= 5 x 6
= 30
RHS = 30
Therefore, LHS = RHS
Hence, we have proved the division property of equality
Division Property of Equality Examples
1. Solve 5x = 40
Solution:
Given Equation: 5x = 40
On dividing 8 from both the side, we get
\[\frac{5x}{8} = \frac{40}{8} \]
\[\frac{5x}{8} \] = 5
5x = 40
x = \[\frac{40}{5} \]
x = 8
To check, we can substitute the value of x in the original equation.
5 x 8 = 40
40 = 40
LHS = RHS
Hence proved
2. Tina brought 100 toffees for ₹ 50. What is the cost of each toffee?
Solution:
Total number of toffees brought by Tina = 100
Cost of 100 toffees = ₹ 50
Let the cost of each toffee be ‘a’. Hence, 100 times ‘a’ is the total cost ₹ 50.
Accordingly, the equation will be
100 a = 50
By dividing both side of the above equation by 10, we get
\[\frac{100}{10} = \frac{50}{10} \]
100 a x 10 = 50 x 10 (Cross multiplication)
1000 a = 500
a = \[\frac{1000}{500} \]
a = 2
To check, we can substitute the value of ‘a’ in the original equation.
500 a = 1000
500 x 2 = 1000
1000 = 1000
LHS = RHS
Hence proved.
In short, the division property of equality states that if we divide both sides of the equation by the same number, the equation remains balanced and equal. Hope you have now understood the division property of equality, now you can easily try questions based on this given on Vedantu’s official website.
FAQs on Division Property of Equality: Definition, Formula & Examples
1. What is the Division Property of Equality in simple terms?
The Division Property of Equality is a fundamental rule in algebra that states if you have a true equation, the equation will remain true if you divide both sides by the same non-zero number. In essence, if two quantities are equal, dividing both by the same amount keeps them equal.
2. What is the formula for the Division Property of Equality?
The formula for the Division Property of Equality can be expressed algebraically. If we have two equal quantities, a and b, such that:
a = b
And we have a non-zero number c (where c ≠ 0), then applying the property gives:
a/c = b/c
This shows that the equality is maintained after division.
3. Can you provide a real-world example of the Division Property of Equality?
Imagine you and your friend have an equal amount of money, say ₹50 each. If you both decide to spend half of your money, you would divide your amount by 2, and your friend would do the same. You would be left with ₹25, and so would your friend. This demonstrates the property: because you started with equal amounts (50 = 50) and divided by the same number (2), you ended up with equal amounts (25 = 25).
4. How is the Division Property of Equality used to solve an algebraic equation?
This property is crucial for isolating a variable in an equation. For example, to solve the equation 4x = 20, your goal is to find the value of 'x'. To do this, you can isolate 'x' by dividing both sides of the equation by its coefficient, which is 4.
- Original equation: 4x = 20
- Apply Division Property: (4x)/4 = 20/4
- Simplify: x = 5
5. Why is it so important that you can only divide by a non-zero number when using this property?
Dividing by zero is mathematically undefined. It doesn't yield a real number or a logical result. If you were to divide by zero on both sides of an equation like 5 = 5, you would get 5/0 = 5/0. Since 5/0 has no meaning, the operation is invalid and breaks the rules of arithmetic. Therefore, the Division Property of Equality strictly excludes division by zero to ensure that all mathematical operations remain valid and logical.
6. How does the Division Property of Equality relate to the Multiplication Property of Equality?
The Division and Multiplication Properties of Equality are inverse operations of each other. While the Division Property helps solve equations like 7x = 49 (by dividing by 7), the Multiplication Property helps solve equations like x/3 = 5 (by multiplying by 3). Essentially, what you undo with division, you can create with multiplication, and vice versa. They are two sides of the same coin, used to isolate variables by performing the opposite operation.
7. Can you give an example of a situation where applying the Division Property of Equality would be incorrect?
A common mistake is applying the operation to only one part of the equation or to only one term on a side. For example, in the equation 2x + 4 = 10, if a student divides only the '2x' term by 2, they get x + 4 = 10, which is wrong. The correct application requires dividing every term on both sides by 2, which would result in:
(2x + 4) / 2 = 10 / 2
x + 2 = 5
This shows that the property must be applied to the entire side of the equation, not just a single term.
8. Where does this property fit within the overall study of algebra?
The Division Property of Equality is one of the four basic Properties of Equality in algebra, alongside the Addition, Subtraction, and Multiplication properties. Together, these properties form the foundation for manipulating and solving linear equations. Mastering them is the first step toward understanding more complex algebraic concepts, as they provide the essential tools for isolating variables and simplifying expressions while maintaining the integrity of an equation.















