




How to Solve Problems Using the Long Division Method
The division is one of the four basic operations of arithmetic, the ways that numbers are combined to make new numbers. The other operations are addition, subtraction, and multiplication.
Long division is one method in which the concept of division, multiplication, and subtraction is used simultaneously.
Not only is this about division, but students must also understand the use of long division, and the meaning of divisors, dividends, and multiples.
In Mathematics, long division problems are the mathematical method for dividing large numbers into smaller groups or parts. It helps to break down a problem into simple and easy steps.
For example, 4 people having pizza now using this application can be divided up into 8 equal parts. Now with this, each person gets 2 slices.


Dividing pizza among 4 people.
Now with this, each person gets 2 slices.
These symbols are used in different forms for example:
x ÷ y
x/y
In this article, long division worksheets and long division problems have been given.
Elements of Division
Here’s one by one element of long division with the following examples.
Dividend- The dividend is the number you are dividing up with
Divisor- The divisor is the number you are dividing by
Quotient- It is the answer
The Remainder- If the answer to the division problem is not a whole number the rest of the number is called the remainder.
Therefore,
Dividend ÷ Divisor = Quotient
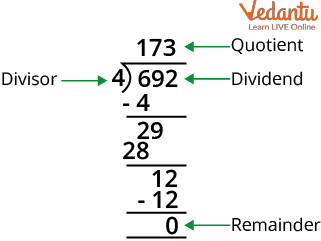
Elements of the Division
Steps to Carry Out in Long Division
We will carry out 5 steps to solve every long division with ease.
Divide
Multiply
Subtract
Bring down
Remainder
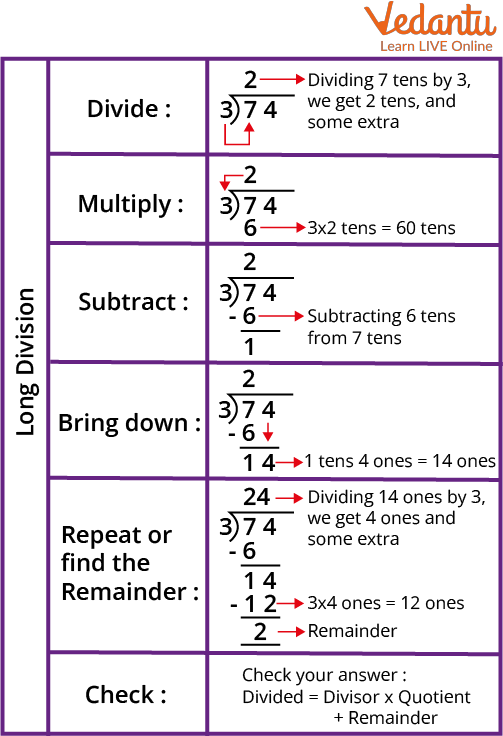
Steps Involved in Long Division
Properties of Long Division
Division by 1 Property: If we divide a number by 1 the quotient is the number itself. Or in other words, when any number is divided by 1, we always get the number itself as the answer/quotient.
For Example:
(i) 7592 ÷ 1 = 7592
(ii) 5247 ÷ 1= 5247
Division by the Same Number Property: If we divide a number by the number itself then the quotient is always 1.
For Example:
(i) 275 ÷ 275 = 1
(ii) 105 ÷ 105 = 1
Division of Any Number by 0 Property is meaningless
For Example:
(i) 35 ÷ 0 = no meaning
(ii) 65 ÷ 0 = no meaning
Division of 0 by Any Number Property: If 0 is divided by a number gives 0 as the quotient or answer. In other words, when 0 is divided by any number, we always get 0 as an answer.
For example:
(i) 0 ÷ 25 = 0
(ii) 0 ÷ 100 = 0
Solved Example of Long Division Worksheet
Example 1: Below is the worksheet to solve the questions by long division methods

Question on Long Division
Ans:

Solution of long division
Example 2: Find the value of quotient and remainder when 75 is divided by 3 ? Verify using the Long division method.
Ans: Here, we divided 75 by 3. So, the dividend is 75 and the divisor is 3.
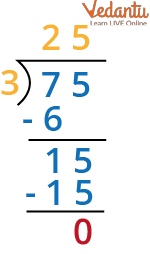
Division of 75 by 3
Hence, we get the quotient as 25 & remainder as 0.
To check division we will put the value.
Dividend = (Divisor × Quotient) + Remainder.
Therefore, 75 = 3 × 25 + 0 = 75
Example 3. Divide 9.24 by 7
Ans:
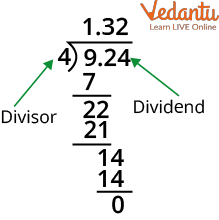
Division with decimal
Practice Problem Related to Long Division
Q1. Divide the 852.8 ÷ 6 and give the exact answer.
Ans: 142.133
Q2. Find the quotient when 7859 is divisible by 76.
Ans: 103.4
Q3. Find the quotient when 91 is divided by 9 using the long division method.
Ans: 10.11
Q4. Divide 324 by 2.
Ans. 162
Summary
All above it is described that long division is a separation of something into different parts. It is a tool that helps to divide things into different parts and it includes elements such as Dividend, Divisor, Quotient, and Remainder. We dealt with the different properties of division and some solutions with solved examples.
FAQs on Long Division Method Made Simple: Step-by-Step Guide
1. What is the long division method and what is its primary importance?
The long division method is a standard algorithm used for dividing large numbers, breaking down a complex division problem into a sequence of easier steps. Its primary importance lies in providing a systematic way to solve division problems that are too difficult to do mentally, especially when dealing with multi-digit divisors or when a remainder is expected. It's a foundational arithmetic skill for tackling more advanced mathematical concepts like polynomial division.
2. What are the main components of a long division problem?
A long division problem consists of four main components:
- Dividend: The number that is being divided.
- Divisor: The number by which the dividend is being divided.
- Quotient: The result or answer of the division.
- Remainder: The amount 'left over' after the division is complete, which is always less than the divisor.
3. What are the 5 key steps to follow in the long division method?
The long division method can be simplified into five recurring steps, often remembered by the acronym DMSBR:
- Step 1: Divide: Divide the first digit (or first few digits) of the dividend by the divisor.
- Step 2: Multiply: Multiply the quotient digit from Step 1 by the divisor.
- Step 3: Subtract: Subtract the product from Step 2 from the part of the dividend you used.
- Step 4: Bring Down: Bring down the next digit of the dividend.
- Step 5: Repeat: Repeat the process from Step 1 with the new number.
4. Can you provide a simple example of solving a problem with the long division method?
Let's solve 145 ÷ 5. First, we see if 5 can go into 1. It can't, so we consider 14. 5 goes into 14 two times (2 x 5 = 10). We write 2 in the quotient. We subtract 10 from 14 to get 4. Next, we bring down the 5, making the new number 45. We divide 45 by 5, which is 9. We write 9 in the quotient. Since 9 x 5 = 45, the subtraction gives a remainder of 0. Thus, the quotient is 29.
5. How does the long division process change when the divisor has two digits?
The fundamental steps (Divide, Multiply, Subtract, Bring Down) remain the same. The main difference is the increased complexity in the 'Divide' step. Instead of dividing by a single digit, you must estimate how many times the two-digit divisor goes into a part of the dividend. This often requires estimation and trial-and-error. For example, to divide by 25, you might think in terms of how many quarters are in a number.
6. What is the main difference between the long division and short division methods?
The main difference lies in how the steps are recorded. In long division, every step of the calculation (multiplication and subtraction) is written down explicitly. This makes it easier to track and is suitable for complex problems. In short division, these calculations are performed mentally, and only the remainders are carried over to the next digit. Short division is faster but is typically used for single-digit divisors where mental maths is more manageable.
7. Why is understanding the 'remainder' important in long division?
Understanding the remainder is crucial because it represents the part of the dividend that cannot be shared equally into groups of the divisor's size. In real-world problems, the remainder has a practical meaning. For example, if you are dividing 25 sweets among 4 friends, the long division gives a quotient of 6 and a remainder of 1. This means each friend gets 6 sweets, and there is 1 sweet left over.
8. In what real-world situations is the long division method useful?
The long division method is useful in many real-world scenarios that involve equal sharing or distribution. For example:
- Splitting a bill of ₹1250 equally among 5 people.
- Calculating how many boxes are needed to pack 500 items if each box holds 25 items.
- Determining the average score over a number of tests or events.
- Converting units, such as calculating how many full dozens are in 180 eggs.
9. Why is it impossible to use zero as a divisor in the long division method?
Using zero as a divisor is impossible because division is the inverse of multiplication. When we ask 'what is 10 divided by 0?', we are asking 'what number multiplied by 0 equals 10?'. Since any number multiplied by 0 is 0, there is no possible answer. Therefore, dividing by zero is undefined in mathematics, and it represents a step that cannot be performed in the long division method or any other form of division.















