




How to Find Multiples: Steps and Practice Questions
Being one of the most exciting chapters of mathematics, Multiples and Factors enables students to get into the fundamentals of calculating and simplifying equations. The chapter establishes a base for students which they can make use of while understanding more difficult areas of this subject. The chapter mainly contains the definition of multiples, how these are important in Mathematics, activity based on common factors and common multiples, etc., along with some examples.
The chapter also contains a detailed description and usage of factors and the differences between common factors and common multiples. These two are vital concepts related to each other; therefore, students should go through both these topics simultaneously to better understand them.
Multiples are an easy way of saying ‘manifold’ or a result of adding something multiple times. It is important that kids learn the meaning and uses of multiples in Maths because this is a concept that will be used in life “multiple times”! So let us learn more about this term.
Definition of Multiple
The term multiple can be defined as the product of a number that is multiplied by another number. A number multiplied by different numbers will result in different multiples. Therefore, a multiple of a number can be reached by multiplying the number by a specific number or by adding the number to itself for a specific number of times.
Examples of Multiples
The number 56 is a multiple of 7. Here, adding 7 eight times will result in the number 56. In other words, multiplying the integer 7 by 8 will give 56. It must be noted here that 56 is also a multiple of 8 since 8 added seven times will give 56 or 8 multiplied by 7 will result in 56.
Here is a table to list a few multiples of 4:
4 x 1 = 4
4 x 2 = 8
4 x 3 = 12
4 x 4 = 16
4 x 5 = 20
4 x 6 = 24
Therefore, it can be said that 4, 8, 12, 16, 20, 24 are all multiples of 4.
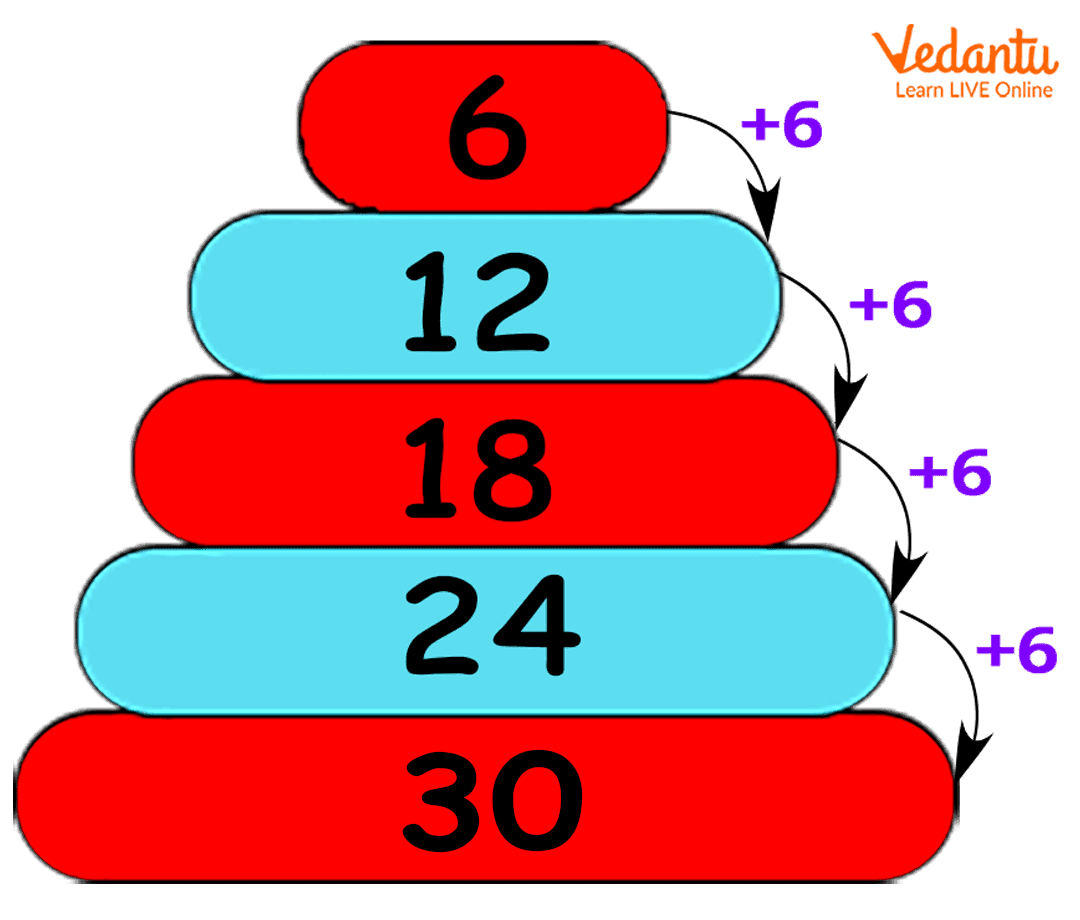
Multiples of 6 by adding 6
Games to Learn Multiples
There is an amazing game which you can play while travelling to school or some other place. This is called the Number plate Game, where you will need to call out the multiples of the first two numbers on the number plate of the vehicle ahead of you. It is a fun way to brush up on your counting skills and become a master of multiples.
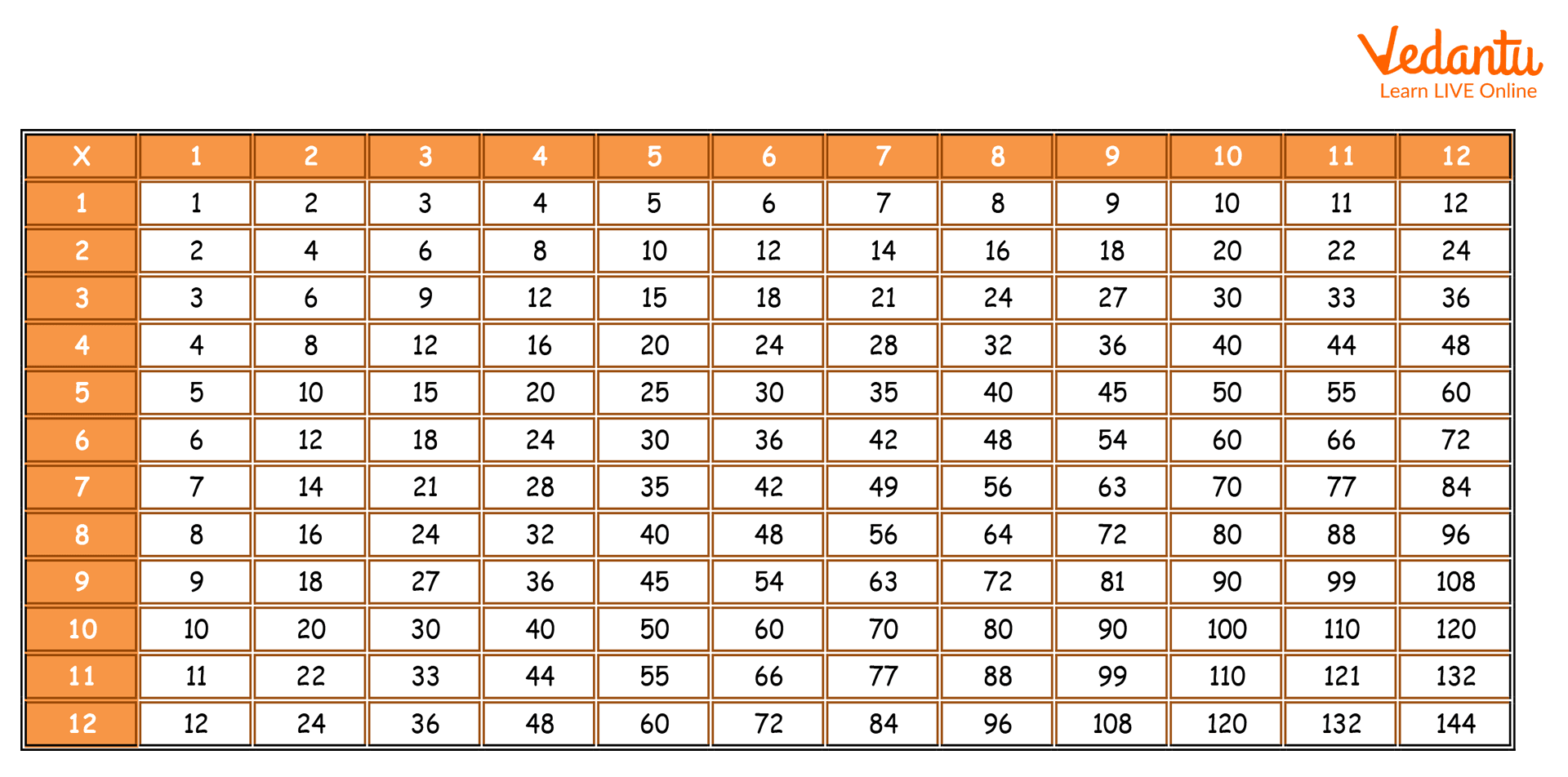
Multiplication table from 1 to 12
What is a Factor?
Factors can be specified as whole numbers that can evenly divide another number. Precisely, when a number is considered as a factor of another second number, the first one has to divide the second number completely without keeping any remainder behind.
In other words, if the dividend is evenly divisible by a number or also called as a divisor, that particular divisor will be known as a factor of that dividend. Every number is supposed to have a common factor, such as one (1) and also the number itself. The highest common factor and lowest common multiple TNPSC questions generally include questions related to these; therefore, students need to go through a few examples to comprehend them.
For instance,
4 is considered as a factor of 24, as it divides 24 evenly and leaves 6 as quotient and zero (0) as remainder. On the other hand, 6 is also considered as the factor of 24, which leaves 4 as quotient and zero (0) as remainder.
Consequently, it is apparent that 24 has multiple factors, such as 1, 24, 4, 6, and 2, 3, 8, including 12, since all these numbers can divide 24 evenly without leaving any remainder.
As discussed earlier, the factor is a number that generally keeps no remainder behind after dividing a particular number. On the other hand, multiple is a number obtained by multiplying a whole number by some other numbers. Following is a list of key differences between common factors and multiples class 4:
Difference Between Common Factors and Common Multiples
Along with these differences, students should also be aware of the process of common factors and common multiples to compare them. Mathematics mainly deals with numbers and different operations, and factors and multiples are one of those kinds. The concepts are pretty basic and should be grasped properly to understand higher-level mathematics in a better way.
Furthermore, with assistance from e-learning platforms like Vedantu, one can elevate their knowledge of multiples. The model exam question papers, expert notes, along with online classes, and doubt clearing sessions, students can better their final exam preparations.
Did You Know?
0 is a multiple of all numbers since any number multiplied by 0 will result in 0!
Conclusion
Multiples are an important part of Maths and the topic should not be avoided or kept for later. It is an integral part of learning counting and calculation, and it is advisable to memorise the multiplication tables at least till 12.
FAQs on What Are Multiples in Maths? Definition, Explanation & Examples
1. What are multiples in Maths? Explain with examples.
In mathematics, a multiple is a number that results from multiplying a given number by an integer (like 1, 2, 3, etc.). In other words, a number is a multiple of another if it can be divided by that number without leaving any remainder. It is essentially the 'answer' in a multiplication table.
For example:
- The multiples of 4 are 4, 8, 12, 16, 20, and so on (4×1, 4×2, 4×3, etc.).
- The multiples of 9 are 9, 18, 27, 36, 45, and so on (9×1, 9×2, 9×3, etc.).
2. How can you find the multiples of any given number?
To find the multiples of any number, you simply need to multiply that number consecutively by the counting numbers (1, 2, 3, 4, 5, ...). The process is the same as reciting the multiplication table for that number. For instance, to find the first five multiples of 8, you would calculate:
- 8 × 1 = 8
- 8 × 2 = 16
- 8 × 3 = 24
- 8 × 4 = 32
- 8 × 5 = 40
So, the multiples are 8, 16, 24, 32, 40, and this list continues infinitely.
3. How are multiples different from factors?
The key difference between multiples and factors is their relationship to the original number.
- Multiples: A multiple is the result of multiplying your number by an integer. Multiples are therefore always equal to or greater than the original number (except for the multiple 0). For example, multiples of 6 are 6, 12, 18, etc.
- Factors: A factor is a number that divides your number exactly, with no remainder. Factors are always equal to or less than the original number. For example, the factors of 6 are 1, 2, 3, and 6.
In short, multiples are about 'multiplying up', while factors are found by 'dividing down'.
4. What are the key properties of multiples?
Multiples have several distinct properties that are fundamental to understanding them:
- Every number is a multiple of itself (e.g., 7 is a multiple of 7 because 7 × 1 = 7).
- Every number is a multiple of 1.
- The first and smallest non-zero multiple of any number is the number itself.
- There are an infinite number of multiples for any given number.
- A non-zero multiple of a number is always greater than or equal to the number.
5. What is a common multiple in math?
A common multiple is a whole number that is a shared multiple of two or more different numbers. To find a common multiple, you list the multiples of each number and identify the numbers that appear in all lists.
For example, to find the common multiples of 3 and 5:
- Multiples of 3 are: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30...
- Multiples of 5 are: 5, 10, 15, 20, 25, 30, 35...
The common multiples of 3 and 5 are 15, 30, and so on. The concept of common multiples is the basis for finding the Least Common Multiple (LCM).
6. Why is it important to learn about multiples?
Understanding multiples is a cornerstone of basic arithmetic and is essential for more advanced mathematical concepts. It is important because it:
- Builds a strong foundation for multiplication and division.
- Is a prerequisite for finding the Least Common Multiple (LCM), which is crucial for adding and subtracting fractions with different denominators.
- Helps in identifying number patterns and solving problems related to time, scheduling, and grouping.
- Enhances overall number sense and problem-solving abilities in algebra and beyond.
7. Is zero a multiple of every number?
Yes, zero is a multiple of every whole number (except for zero itself, as division by zero is undefined). This is a special case that can sometimes be confusing. A number is a multiple of another if it can be produced by multiplying that number by an integer. Since any number multiplied by the integer 0 results in 0, zero is a valid multiple.
For example:
- 9 × 0 = 0, so 0 is a multiple of 9.
- 25 × 0 = 0, so 0 is a multiple of 25.
8. Where are multiples used in everyday life?
Multiples are used frequently in real-world scenarios, often without us realising it. Some practical examples include:
- Event Planning & Scheduling: If you need to plan an event where one service visits every 3 days and another every 4 days, finding a common multiple (like 12) tells you when they will both be there on the same day.
- Shopping in Bulk: To buy an equal number of hot dogs (sold in packs of 10) and buns (sold in packs of 8), you need to find the least common multiple to avoid waste.
- Time Management: Calculating when you'll next have a meeting that occurs every 2 weeks is an application of multiples.















