Relative Speed in Opposite Direction Explained

Do you know the meaning of relative speed? A moving body's relative speed is its speed in relation to another. It is possible to shorten the word "Relative" to "in comparison with". Two bodies' differences are used to determine their relative speeds while they are travelling in the same direction. However, when two bodies are travelling in opposition to one another, the relative speed is calculated by adding the speeds of the two bodies.

How to Calculate Relative Speed?

Keep in mind that the two bodies that are moving at different speeds but in the same general direction.

Assume the first body's speed be x km/hr and the second body's speed be y km/hr.

The relative speed will be $\left( {x - y} \right)$ km/hr

The moment both bodies eventually meet $= \dfrac{{{\rm{Travel \,distance}}}}{{{\rm{Relative\, speed}}}} = \dfrac{{d\,{\rm{ km}}}}{{\left( {x - y} \right){\rm{ km/hr}}}}$

Knowing that relative speed is the speed of one object in relation to another object.

Therefore, once the time for the meeting of both bodies is given,

Suppose time = t hrs

Then distance covered in t hours $= {\rm{Relative \,speed}} \times {\rm{Time}} = \left( {x - y} \right){\rm{ km/hr}} \times t{\rm{ hrs}}$

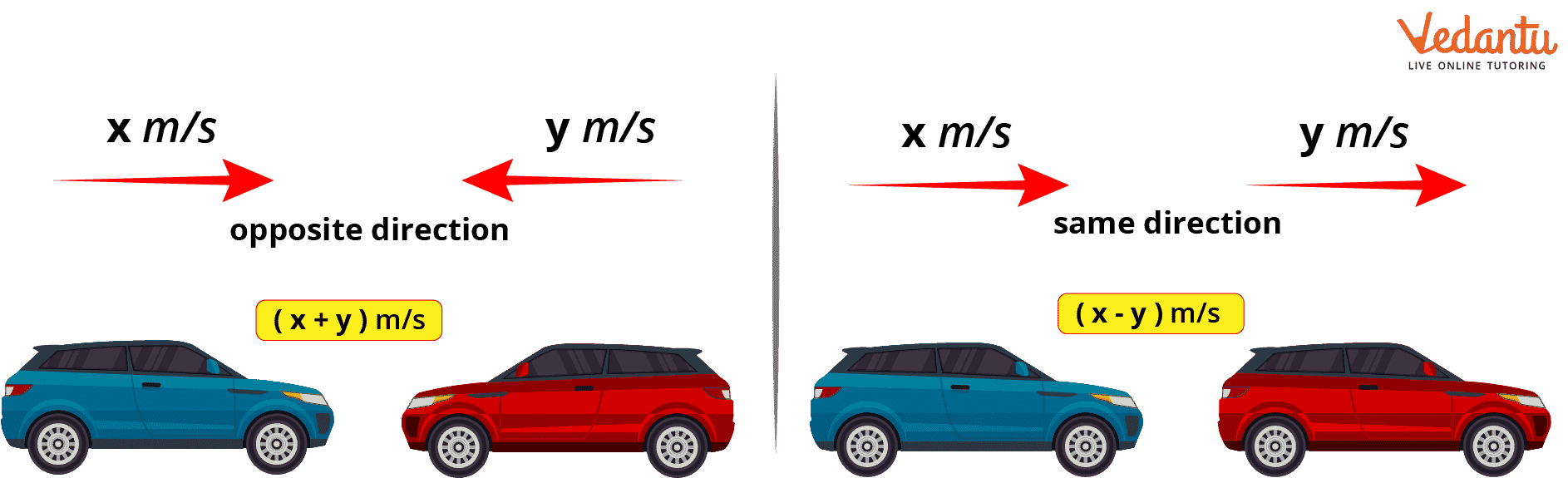
Relative Speed in the Same and Opposite Direction

Formula for Relative Speed:

The formula below demonstrates how to determine a moving object's constant velocity using the conventional approach.

$r = \dfrac{d}{t}$

Where, r is rate of speed, d is distance travelled and t is time.

The above equation determines the average speed of an object over time. The object may move more quickly or more slowly at certain points over the time period. The average speed of an object is equal to the total distance travelled divided by the total time travelled.

• The difference in the speeds of two bodies moving in the same direction can be used to calculate their relative speed. It can be described as ${V_1} - {V_2}$.

• The total of the speeds of two bodies can be used to calculate their relative speed when they are going in the opposite direction at different speeds. It can be described as ${V_1} + {V_2}$.

Examples on Concept of A and B Start from a Point in Opposite Direction

Example 1: A telegraph post is crossed by two trains of identical length in 10 and 15 seconds, respectively. Assuming that each train is 120 metres long. When will they cross each other in opposing directions, in seconds?

Solution:

Speed of first train = $\dfrac{{120}}{{10}} = 10m/s$

Speed of second train = $\dfrac{{120}}{{15}} = 8m/s$

Therefore, their relative speed $ = 12 + 8 = 20m/s$

Therefore, required time $\begin{array}{l} = \dfrac{{120 + 120}}{{20}} = 12\sec \end{array}$

Hence, the two trains cross each other in 12 seconds.

Example 2: A man is walking at a speed of 5 km/hr in the opposite direction from a train that is moving at 45 km/hr. What is the length of the train if it passes the man in 18 seconds?

Solution:

The man is approaching the speeding train from the opposite direction, thus:

$\text{Relative speed of train} = \left( {45 + 5} \right)km/hr\\ \Rightarrow \text{Relative speed of train} = \left( {50 \times \dfrac{5}{{18}}} \right)m/s\\ \therefore \text{Relative speed of train} = \dfrac{{250}}{{18}}\,m/s$

$\Rightarrow \text{Length of train} = {\rm{Relative \,speed}} \times {\rm{Time \,taken}}\\ \Rightarrow \text{Length of train}{\rm{ = }}\dfrac{{250}}{{18}} \times 18\\ \therefore \text{Length of train}= 250\,m$

Hence, the length of the train is 250 m.

Example 3: Running from the same location with speeds of 10 km/h and 5 km/h respectively are two athletes. If they move in the opposite direction, how far apart are they after 20 minutes?

Solution:

Speed of 1^st athlete = 10 km/hr

Speed of 2^nd athlete = 5 km/hr

Relative speed $ = \left( {10 + 5} \right)km/hr$

Time taken $ = 20\min = \dfrac{{20}}{{60}} = \dfrac{1}{3}$

$\text{Distance} = {\rm{Relative \,speed}} \times {\rm{Time \,taken}}\\ \Rightarrow \text{Distance}{\rm{ = 15km/hr}} \times \dfrac{1}{3}hr\\ \therefore \text{Distance} = 5\,km$

Hence, the two athletes are 5 km apart after 20 minutes.

Conclusion

This article helped us to learn the basic concept of relative speed. The basic definition of relative speed is explained. A brief idea about the topic is achieved. Also, some examples are studied which can help in solving real-life problems. The formula for relative speed is known and can be used to solve the questions related to relative speed. The topic of relative speed is important for learning as many day to day life problems can be solved using the understanding of this topic.