Tangent Secant Theorem Explained

The tangent-Secant Theorem formula is a fundamental tool of Geometry found in Euclid’s Elements book. There are many methods to prove the theorem. Most important is using similar triangles. So, in this article, we will be discussing the proof of the Theorem in detail and its applications.

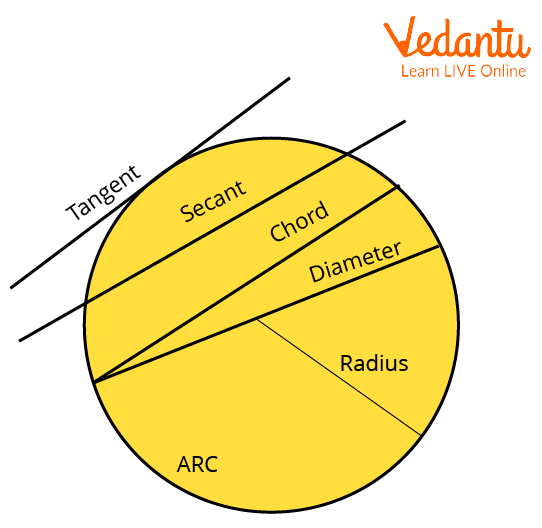
Terms Associated with Circle

History of Euclid

Euclid

Name: Euclid

Born: Mid-4th century BC

Died: Mid-3rd century BC

Field: Mathematics

Nationality: Greek

Statement of Tangent-Secant Theorem

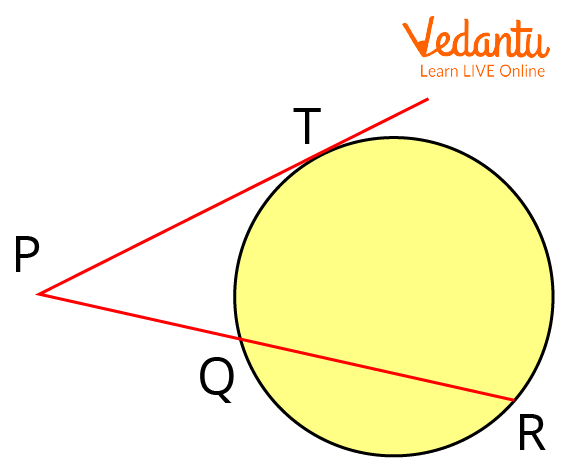
Circle with PT tangent and PQR secant

For a circle with centre O, consider PT to be the tangent to the circle at the point from external point P and PQR to be the secant to the circle with points Q and R on the circle, then Tangent-Secant Theorem is defined as:

$P Q \times P R=P T^{2}$

Proof of Secant Tangent Theorem

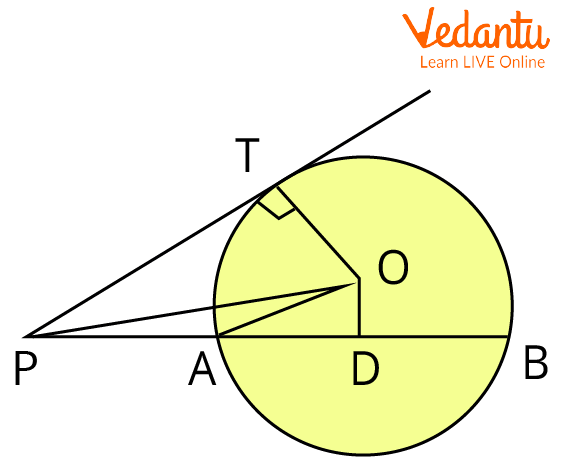
Proof of the Tangent Secant Theorem

Given: PAB is secant to the circle with centre 0 and radius r. PT is tangent to the circle.

To prove: $P A \times P B=P T^{2}$

Construction: Draw $O D \perp A B$. Join $O P, O T$, and $O A$.

Proof:

Since $O D \perp A B$

$\therefore A D=D B \ldots(1)$ (Perpendicular from the centre to the chord bisects the chord)

$P A \times P B=(P D-A D)(P D \div B D)$

$\Rightarrow P A \times P B=(P D-A D)(P D+A D) \quad$ (Using 1)

$\Rightarrow P A \times P B=P D^{2}-A D^{2}$

In right $\triangle O P D$,

$O P^{2}=O D^{2}+P D^{2}$

$\Rightarrow P D^{2}=O P^{2}-O D^{2}$

$\therefore P A \times P B=\left(O P^{2}-O D^{2}\right)-A D^{2}$

$\Rightarrow P A \times P B=O P^{2}-\left(O D^{2}+A D^{2}\right)$

In right $\triangle O A D$,

$O A^{2}=O D^{2}+A D^{2}$

$\therefore P A \times P B=O P^{2}-O A^{2}$

$\Rightarrow P A \times P B=O P^{2}-O T^{2} \quad(\because O A=O T)$

In $\triangle O P T$,

$O P^{2}=P T^{2}+O T^{2}$

$\Rightarrow O P^{2}-O T^{2}=P T^{2}$

$\therefore P A \times P B=P T^{2}$

Hence proved.

Limitations of Tangent-Secant Theorem

1. The tangent-Secant theorem doesn’t give any idea if the secant and tangent are not drawn from common points.

2. Tangent-Secant Theorem is only applicable in the case of 2-dimensional circles and not in 3-dimensional figure spheres.

Applications of Tangent-Secant Theorem

• Tangent-Secant Theorem is of great significance. It is used in our day-to-day life such as school buildings, bridges, monuments etc.

• Monuments such as the Statue of Liberty and Pyramids are also based on concepts of secants and tangents.

Solved Examples

1. In the given figure, $P Q=12 \mathrm{~cm}, P T=24 \mathrm{~cm}$, then find $R Q$.

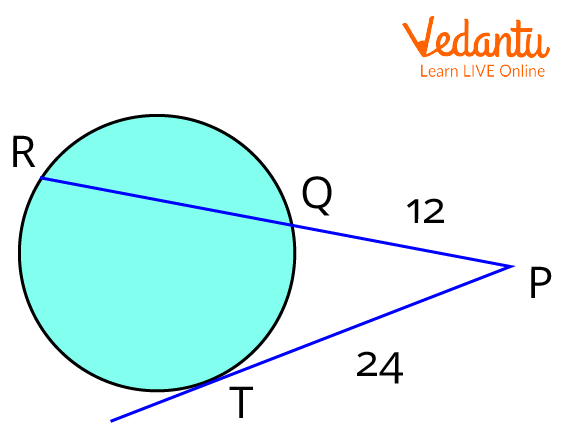
PQ and Tangent PT is given

Ans:

Using Tangent Secant Theorem, we have

$P Q \times P R=P T^{2}$

Putting values, we get

$(12+x) \times 12=24^{2} \\$

$\Rightarrow(12+x) \times 12=576 \\$

$\Rightarrow(12+x)=48 \\$

$\Rightarrow x=48-12 \\$

$\Rightarrow x=36$

So, we get

$R Q=36 \mathrm{~cm}$

2. In a circle, the tangent is drawn from outside point $P$ to the circle at point $T$ and from the same point secant is drawn to the circle intersecting the circle at $Q$ and $R$, respectively, such that $P Q=25 \mathrm{~cm}, R Q=9 \mathrm{~cm}$, then find $P T$.

Ans:

According to the question, we get the following figure:

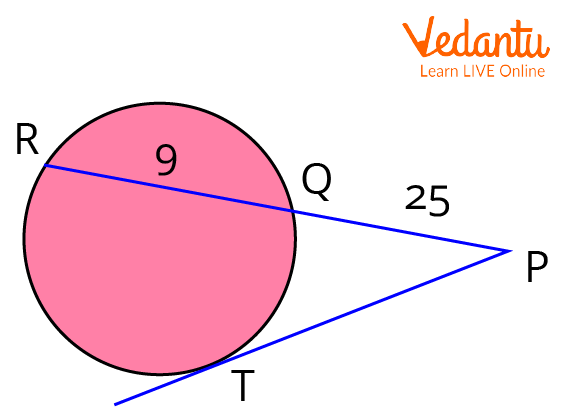
Secant PQR is given

Using Tangent Secant Theorem, we have

$P Q \times P R=P T^{2}$

Putting values, we get

$(25+9) \times 25=P T^{2} \\$

$\Rightarrow P T^{2}=34 \times 25$

$\Rightarrow P T^{2}=850 \\$

$\Rightarrow P T=\sqrt{850} \\$

$\Rightarrow P T=29.154$

So, we get

$P T=12.154 \mathrm{~cm}$

3. In the given figure, $P R=84 \mathrm{~cm}, P T=42 \mathrm{~cm}$, then find $R

Q$.

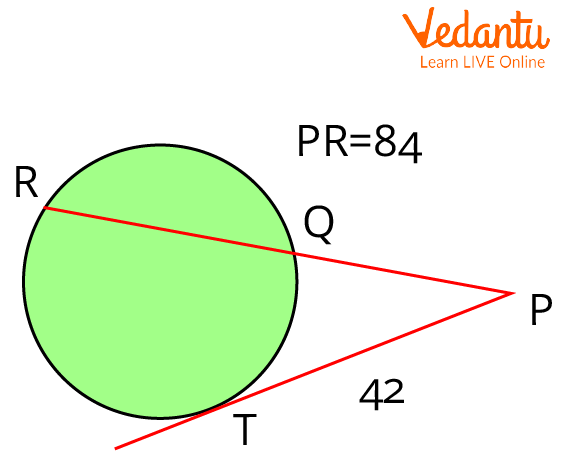
Secant and tangent from a point are given

Ans:

Using Tangent Secant Theorem, we have

$P Q \times P R=P T^{2}$

Putting values, we get

$P Q \times 84=42^{2} \\$

$\Rightarrow P Q \times 84=1764 \\$

$\Rightarrow P Q=21$

Now,

$R Q=P R-P Q$

And,

$P Q=21 \\$

$\Rightarrow R Q=84-21 \\$

$\Rightarrow R Q=63 \mathrm{~cm}$

Important Formulas to remember

• $P Q \times P R=P T^{2}$, where $\mathrm{PT}$ is tangent and $\mathrm{PQR}$ is secant to the circle with centre $O$ and radius $r$.

Important Points to Remember

• A Tangent line touches the circle at only one point.

• A Secant line touches the circle at exactly two points.