




How Does a Circular Loop Produce a Magnetic Field?
With the help of magnetic field lines, we can visualise the magnetic field. The pattern of the magnetic field lines depends on the shape of the magnet. The magnetic field lines give us the pattern of the magnetic field. Using iron filings or a magnetic compass, we can find the shape of the magnetic field.
In this article, we will get a deep insight into the magnetic field produced by a current carrying circular loop and Maxwell’s right hand thumb rule to find the direction of the magnetic field.
History of Magnetism
Magnetism has been known since ancient times. In 1820, Hans Christian Oersted invented a very useful phenomenon. He was born in Rudkobing, Denmark. He observed that when the electric wire carries electric current, it behaves like a magnet. He established the relation between electricity and magnetism in the 19th Century. He played a crucial role in understanding electromagnetism.
What is a Magnetic Field?
The region surrounding the magnet in which the force of the magnet can be felt is called the extent of the magnetic field. Its SI unit is Tesla and it is named after the American Scientist Nikola Tesla. Gauss is the smaller unit of the magnetic field.
Magnetic field lines generally originate from the North Pole of the magnet and end at the South Pole but inside the magnet, magnetic field lines are directed from the South Pole to the North Pole. Thus, we can say that magnetic field lines form a closed curve. They can never intersect with each other.
Magnetic Field Due to Current Carrying Circular Loop
The magnetic field lines due to current through a circular loop is shown in the figure given below.
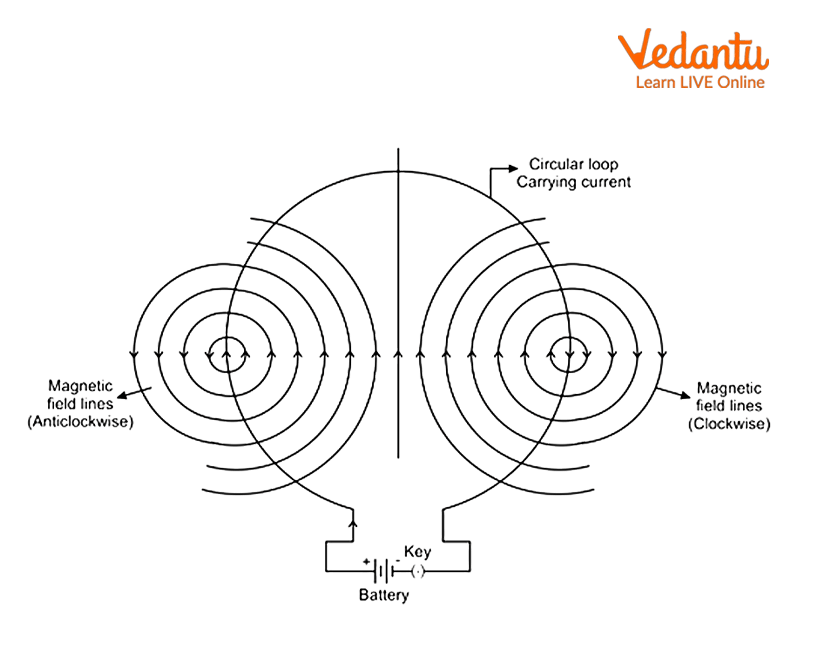
Magnetic Field Due to Current Carrying Circular Loop
Circular loop is a collection of many straight lines. Here, one end of a circular loop is connected to a positive end of a battery and another end is connected with the negative end of the battery. So, current can flow and in the circular loop, it is moving in clockwise direction as shown in above figure. We know that when current flows in a conductor, the magnetic field will get generated which can produce magnetic field lines.
We can observe that the magnetic field lines are in the form of concentric circles near the sides of the loop but towards the centre of the loop, the magnetic field lines become almost parallel which indicates that this part of the coil has a uniform magnetic field. In other words, we can say that at the centre of the circular loop, magnetic field lines become straight lines. At every point of a loop, the concentric circles representing the magnetic field around it would become larger and larger as we move away from the loop. The strength increases as we go closer to the centre of the loop.
In the case of the straight current carrying wire, if we know the direction of current, we can find the direction of the magnetic field using Maxwell’s right hand thumb rule. This rule can be applied for finding the direction of magnetic field of this current carrying loop as well.
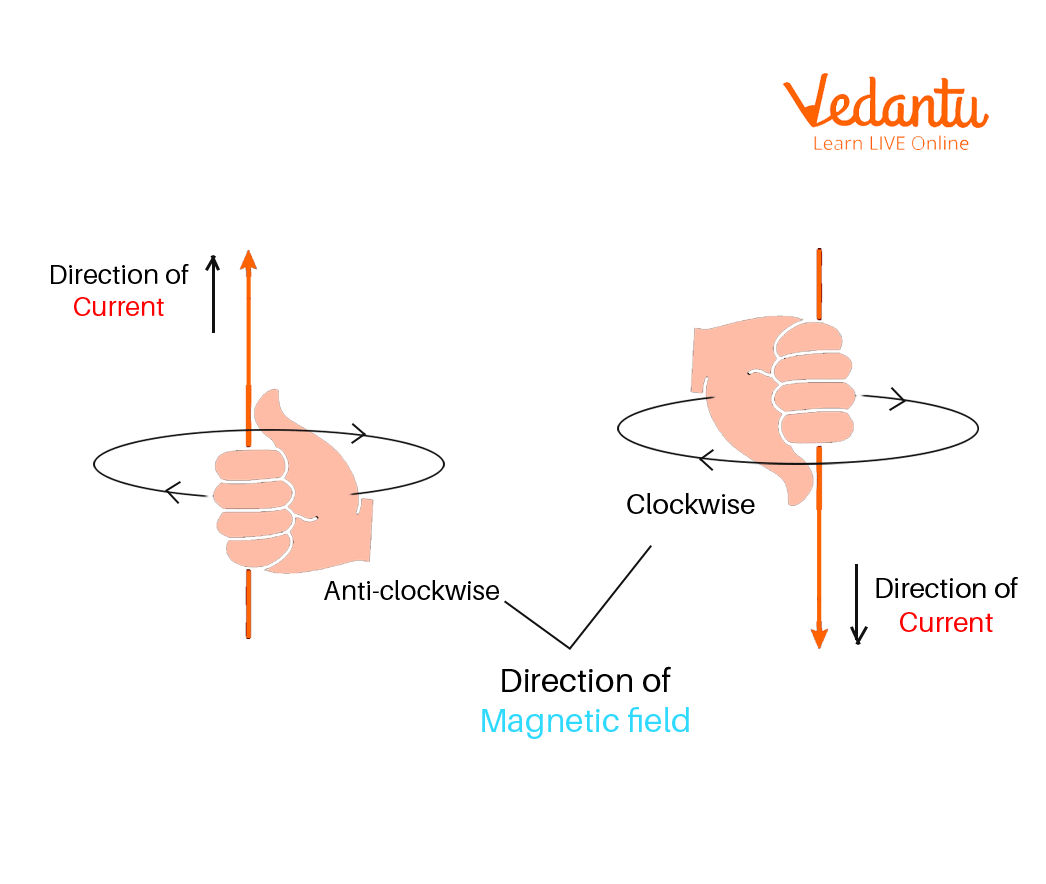
Maxwell’s Right Hand Thumb Rule
This rule says that if your thumb represents the direction of current, then the direction in which all other four fingers are curled represent the direction of the magnetic field. So, in order to apply the right-hand thumb rule, hold a loop in your right hand such that your thumb points the direction of current in this loop, then the direction in which fingers are wrapped around the loop is the direction of the magnetic field. This is shown in the above figure.
By applying this rule, we find that each small section of the circular loop contributes to the magnetic field lines in the same direction within the loop. This is how a current carrying loop behaves.
The magnetic field intensity due to current carrying circular loop (at the centre) is given by,
\[B = \dfrac{{{\mu _0}NI}}{{2r}}\]
Where, ${\mu _0} = 4\pi \times {10^{ - 7}}Tm{A^{ - 1}}$ and it is the permeability of free space
$I$ is the current flowing in the loop
$r$ is the radius of the loop
$N$ is the number of turns of the loop
Factors on Which the Magnetic Field Produced by a Current Carrying Circular Loop Depend
The magnetic field produced by this current carrying circular loop at a given point is
Directly proportional to the amount of current flowing through it.
This means B is proportional to I
Directly proportional to the number of turns of the loop.
This means N is proportional to I
This happens because the current in each turn would be in the same direction. Hence, the field due to these adds up.
Inversely proportional to the radius of the loop.
This means B is inversely proportional to 1/r
Solved Examples
A tightly wound 100 turn coil of radius $10cm$ is carrying a current of $1A$
Find the value of the magnetic field at the centre of the coil.
Ans: Given: Radius of the coil is $r = 10cm = 10 \times {10^{ - 2}} = 0.1m$
$I = 1A$
${\mu _0} = 4\pi \times {10^{ - 7}}Tm{A^{ - 1}}$ is the permeability of free
space
Number of turns $N = 100$
The value of the magnetic field at the centre of the coil is given by,
$B = \dfrac{{{\mu _0}}}{2}\dfrac{{NI}}{r}$
Substituting the given values in above equation,
We will get, $B = \dfrac{{4\pi \times {{10}^{ - 7}}}}{2}\dfrac{{100 \times 1}}{{0.1}}$
$\therefore B = 6.28 \times {10^{ - 4}}T$
So, the value of the magnetic field is $6.28 \times {10^{ - 4}}T$
An $\alpha $ particle is completing one circular round of radius $0.8m$ in 2 seconds. Find the magnetic field at the centre of the circle. (Given: electronic charge $e = 1.6 \times {10^{ - 19}}C$ )
Ans: Given: Radius of circle is $r = 0.8m$
Time taken is $t = 2\sec $
We know that ${\mu _0} = 4\pi \times {10^{ - 7}}Tm{A^{ - 1}}$ is the permeability of free space
The charge $q$ on $\alpha $ particle is $2e = 2 \times \left( {1.6 \times {{10}^{ - 19}}} \right) = 3.2 \times {10^{ - 19}}$
The amount of charge which flows through any conductor per unit time is known as current and we can express it by $I = \dfrac{q}{t} = \dfrac{{2e}}{t}$
Substituting the values in above equation,
We will get, $I = \dfrac{{3.2 \times {{10}^{ - 19}}}}{2} = 1.6 \times {10^{ - 19}}A$
Magnetic field at the centre of the circle is given by, $B = \dfrac{{{\mu _0}I}}{{2r}}$
Substituting the values in above equation,
We will get, $B = \dfrac{{\left( {4\pi \times {{10}^{ - 7}}} \right) \times \left( {1.6 \times {{10}^{ - 19}}} \right)}}{{2 \times 0.8}} = 12.57 \times {10^{26}}T$
The value of magnetic field at the centre of the circle is $12.57 \times {10^{ - 26}}T$
Interesting Facts
The South Pole of the Earth’s magnet is in the geographical North and the North Pole of the Earth's magnet is in the geographical South.
Magnetite is the most magnetic natural metal on the Earth.
Magnets generate a non-contact force. The force which acts without physical contact between two objects is called non-contact force. In this type of force, physical contact is not required.
Conclusion
From the above discussion, we can conclude that when we reach the centre of the loop, the magnetic field at the centre of a circular coil appears to be straight line. The strength of the magnetic field decreases with an increase in distance from the loop. We have also discussed the factors affecting the magnetic field produced by a current carrying circular loop and some interesting facts. We hope to have helped you with your queries and doubts.
FAQs on Magnetic Field Due to a Current in a Circular Loop
1. What is the magnetic field due to a current in a circular loop?
When an electric current flows through a circular wire loop, it generates a magnetic field in and around the loop. The magnetic field lines are nearly circular near the wire but become straight and perpendicular to the plane of the loop at its center. This arrangement effectively creates an electromagnet, with one face of the loop acting as a North pole and the other as a South pole, depending on the direction of the current flow.
2. What rule determines the direction of the magnetic field for a current-carrying circular loop?
The direction of the magnetic field is determined by the Right-Hand Thumb Rule (also known as the Right-Hand Grip Rule). If you curl the fingers of your right hand in the direction of the current flowing through the loop, your thumb will point in the direction of the magnetic field at the center of the loop. For example, if the current is flowing in an anti-clockwise direction, the magnetic field points outwards, and that face of the loop acts as a North pole.
3. What is the formula for the magnetic field at the center of a circular loop carrying current?
The magnitude of the magnetic field (B) at the center of a circular loop with radius 'R' carrying a current 'I' is given by the formula:
B = (μ₀ * I) / (2 * R)
Where:
- B is the magnetic field strength.
- μ₀ is the permeability of free space (a constant value of 4π × 10⁻⁷ T·m/A).
- I is the current flowing through the loop.
- R is the radius of the loop.
4. How is the magnetic field calculated at a point on the axis of a circular current loop?
To calculate the magnetic field (B) at a point 'P' on the axis of a circular loop at a distance 'x' from its center, we use the following formula derived from the Biot-Savart Law:
B = (μ₀ * I * R²) / (2 * (R² + x²)^(3/2))
Where 'R' is the loop's radius and 'I' is the current. At the center of the loop (where x=0), this formula simplifies to the one for the magnetic field at the center.
5. How does a circular current loop behave like a magnetic dipole?
A circular current loop acts as a magnetic dipole because its magnetic field pattern at large distances is identical to that of a bar magnet. One face of the loop acts as a North pole and the other as a South pole. The loop has a magnetic dipole moment (M) given by M = I * A, where 'I' is the current and 'A' is the area of the loop (πR²). The direction of the magnetic moment vector is perpendicular to the plane of the loop, determined by the Right-Hand Thumb Rule.
6. Why is the magnetic field strongest at the center of a circular loop?
The magnetic field is strongest at the center because at this point, the magnetic field contributions from all the small current elements (dl) of the loop add up constructively and are directed along the axis. As you move away from the center along the axis, the distance from the wire elements increases, and the components of the magnetic field perpendicular to the axis start to cancel each other out, resulting in a weaker net magnetic field.
7. What are some real-world applications of the magnetic field from a circular loop?
The principle of the magnetic field from circular loops is fundamental to many devices. Some key applications include:
- Solenoids and Electromagnets: A solenoid is essentially a series of many circular loops, creating a strong, uniform magnetic field inside.
- Galvanometers: These devices use the torque experienced by a current-carrying coil (loop) in a magnetic field to measure electric current.
- Electric Motors: The rotational force on a current loop in a magnetic field is the core principle behind electric motors.
- Magnetic Resonance Imaging (MRI): Powerful electromagnets, based on coils of wire, are used to generate the magnetic fields needed for medical imaging.
8. How does the magnetic field of a circular loop differ from that of a long, straight wire?
There are key differences in their magnetic field patterns:
- Field Line Shape: For a straight wire, the magnetic field lines are concentric circles around the wire. For a circular loop, the field lines pass through the center of the loop, creating a pattern similar to a bar magnet.
- Field Strength: The magnetic field of a straight wire decreases with distance (B ∝ 1/r). The field of a circular loop is concentrated and strongest at its center.
- Poles: A circular loop creates distinct North and South poles on its faces, behaving like a dipole. A straight wire does not have poles in the same sense.
9. What would happen to the magnetic field at the center of a loop if the current is doubled and the radius is halved?
The magnetic field at the center is given by B = (μ₀ * I) / (2 * R).
If the new current I' = 2I and the new radius R' = R/2, the new magnetic field B' will be:
B' = (μ₀ * I') / (2 * R') = (μ₀ * 2I) / (2 * (R/2)) = (μ₀ * 2I) / R = 4 * [(μ₀ * I) / (2R)] = 4B.
Therefore, the magnetic field at the center would become four times its original strength. This demonstrates the strong dependence of the field on both current and radius.






















