Torque Explained: Concepts, Formulas & Applications

In Physics, torque is just the tendency of a force to turn or twist. Completely different terminologies like moment or moment of force are interchangeably used to describe torque. The distance of the point of application of force from the axis of rotation is typically known as the moment arm or lever arm.

This concept originated with the studies of Archimedes of usage of levers. In rotational mechanics, torque takes the place of force in linear kinematics. When you open a door, the torque applied within the situation permits it to move round the rotational axis.

What is Torque?

Torque is a measure of the force that may cause an object to rotate around an axis. As force is what causes an object to accelerate in linear kinematics, torque is what causes an object to acquire angular acceleration and it is a vector quantity. A force applied perpendicularly to a lever multiplied by its distance from the length of the lever arm is its torque.

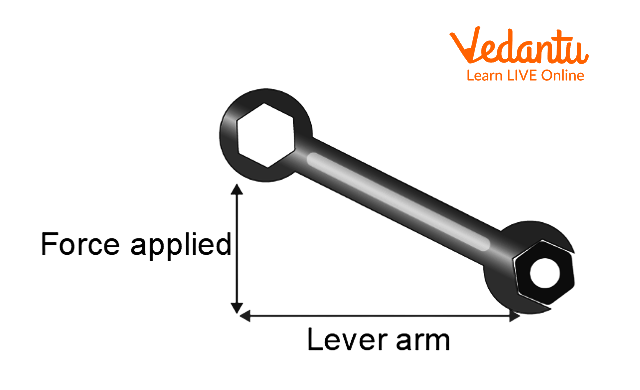
Torque

Types of Torque

Torque can be both:

• Static torque

• Dynamic torque

Static Torque

A static torque is one which does not produce an angular acceleration. Someone pushing on a closed door is applying a static torque to the door because the door is not rotating approximately its hinges, despite the force applied. Someone pedalling a bicycle at constant speed is also applying a static torque because they're not accelerating.

Dynamic Torque

The drive shaft in a racing car accelerating from the start line is carrying a dynamic torque as it should be producing an angular acceleration of the wheels given that the car is accelerating along the track.

Equation of Torque

The magnitude of the torque vector for a torsion created by a given force (F) is :

$\tau = r \times F = r \,F \,sin\theta$

$\tau$ = torque

F = linear force

r = distance measured from the axis of rotation to where the application of linear force takes place

$\theta$= the angle among F and r

In this system, sinθ has no units, r has units of metres (m), and F happens to have units of Newtons (N). Combining these together, one can see that a unit of torque is a Newton-metre (Nm).

The SI unit for torque happens to be the newton-metre (N⋅m).

Now let’s find the formula or expression.

Rate of change of Angular Momentum when it comes to time = $\dfrac{\Delta L}{\Delta T}$

Now, $\dfrac{\Delta L}{\Delta T}=\dfrac{\Delta I\omega }{\Delta T}=I\cdot \dfrac{\Delta \omega }{\Delta T}$……. (1)

Here, I is certainly constant when the mass and shape of the item are unchanged.

Now $\dfrac{\Delta \omega }{\Delta T}$ refers to the rate of change of angular velocity with time i.e. angular acceleration ($\alpha$). So from equation four one can write,

$\dfrac{\Delta L}{\Delta T}=\alpha I$…………………(2)

I (moment of inertia) refers to the rotational equivalent of mass(inertia) of linear motion. Similarly, angular acceleration \alpha (alpha) certainly refers to the rotational motion equal to linear acceleration.

Torque ($\tau$) refers to the moment of force.

$\tau = r \times F = r \,F \,sin\theta$ ……………. (3)

Here, F is the force vector and r refers to the position vector and $\theta$ takes place to be the angle between the force vector and the lever arm vector. ‘x’ certainly denotes the cross product.

$\tau = r F sin \theta$

We know that according to Newton's Second law,

$F=ma$

$\Rightarrow \tau = r \,ma \,sin\theta$

$\Rightarrow \tau = r \,m \,\alpha \,r \,sin\theta$

$\Rightarrow \tau = m\,r^2\, \alpha \,sin \theta$

$\Rightarrow \tau= I\, \alpha \, sin\theta = \text{I}\times \alpha$ ………… (4)

$\theta$ is angular acceleration, I refer to the moment of inertia and X denotes cross product.

$\tau = I \alpha$.......(from equation 4)

$\tau = I \times \dfrac{(ω_2 – ω_1)}{t}$

here $\alpha$ = angular acceleration = time rate of change of the important angular velocity = $\dfrac{(ω_2 – ω_1)}{t}$

where $ω_2$ and $ω_1$ happen to be the final and initial angular velocities and t is the time gap or T

$\tau = I\,(ω_2 – ω_1)$ …………(5)

when, T = 0 (i.e., net torque is zero),

$I (\omega_2 - \omega_1)$ = 0

i.e., $I\omega_2=I \omega_1$…….. (6)

So from equation two and 4 one can get, $\dfrac{\Delta L}{\Delta T}=\tau$ , this certainly states that the rate of change of angular momentum with time is referred to as Torque.

A torque may be a twist of an item around a given axis, almost like how a linear force is a push or a pull. The product of the magnitude of the force and therefore the perpendicular distance of the line of action of a force from the axis of rotation is another definition of torque.

Measurement of Torque

The unit of torque is Newton and metre (N.m). The equation for torque is represented as the vector product of force and position vector. Using vector product notations, we will find the direction of torque.

$\tau = r \times F$

Measurement of Torque

Measuring a static torque during a non-rotating system is sometimes quite straightforward, and done by measuring a force. Measuring torque during a rotating system is significantly harder. One technique works by measuring strain within the metal of a drive shaft which is transmitting torque and causing this information wirelessly.

Examples of Torque

Some of the examples of torque are listed as follows:

• Opening a bottle cap

• Rotating the steering wheel of the car

• Screwing the bolt and nut the usage of a wrench and nutcracker

• Playing See-saw

• Twisting the taps

• Opening the doors

Solved Problems

1. A classroom door has a width of 80 cm. If the handle of the door is 30 cm from the edge and the Force of 8 N is applied on the handle, calculate the torque.

Ans. The distance of the handle of the door from edge = 30 cm.

Therefore, the line of action is 30/2 = 15 cm.

Measurement of the lever arm = d = 80 – 15 = 65 cm = 0.65 m

Force exerted = 8N

Torque = F × d= 8 × 6.5

Torque = 52 Nm.

Hence, the value of torque is 52 Nm.

2. The width of a door is 50 cm. If it is released with force of 2 N away from the hinges, calculate the torque produced which causes the door to open.

Ans: Force applied , F = 2 N

d is the length of the lever arm , that is 50 cm.

Measurement of lever arm in m = 0.50 m

Torque = F × d = 0.50 × 20

Torque = 10 Nm.

Hence, the value of torque is 52 Nm.

Conclusion

Just as a linear force is a push or a pull, a torque can be thought of as a twist to an object around a specific axis. It is also defined as the torque is the product of the magnitude of the force and the perpendicular distance of the line of action of a force from the axis of rotation. Given the length of the moment arm, the torque may be found directly. Measurement of torque and its applications are mentioned within the above article.