




Key Concepts and Applications of Turning Forces
To turn or spin something around, forces are required. Moving objects move in straight directions when left unattended. Instead, turning them in a circle requires a force. Larger forces are required to rotate larger objects. Make them spin faster or in smaller, more precise circles.
Real-world examples of the turning effect of forces include pushing a door open, swinging on a see-saw, and pedalling a bicycle. When you can understand what actually occurs in real life, it appears to be rather straightforward. We will learn more about turning forces in this article. Let’s dive in and learn about turning forces.

Two Children on a see-saw
Relate Problems to Real-life Scenarios
There are a few highly prevalent instances of the forces turning in our daily lives. It will be simpler to visualise what is happening if you try to draw comparisons between the questions on your worksheet and real-world situations we have encountered. If you're still not sure what the turning effect of forces is all about, think of a see-saw.
You are aware that two equal-weight individuals must sit at either end of the see-saw to keep it balanced. You could claim that both forces are exerting the same amount of pressure on the see-saw.
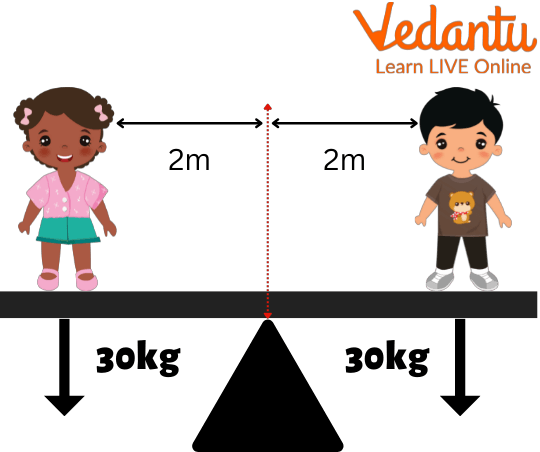
Turning Effect on a see-saw
But what if one of the people—with the same weight!—was moved closer to the see-pivot saw's point? The person's side will incline downward, appearing heavier. Take note of the fact that the distance from the pivot, in addition to weight, affects how much a difference there is.

One Kid Moved Closer to the Centre
Consider how you could balance the see-saw while maintaining the same positions as in the second scenario. One method is to put more weight on the person closest to the pivot.

More Weight on One Side
The Formula for Turning Effect of Forces
As you can see, two factors—distance from the pivot and weight of the person—influence the force acting upon the see-saw.
Observation 1: The turning effect rises with distance from the pivot for an equal weight applied.
Observation 2: As the weight applied rises, the turning effect grows at a constant distance from the pivot.
Putting two and two together, we arrive to the following equation:
Weight (N) x Distance (m) = Turning effect (Nm)
It's crucial to understand that the turning effect of forces is also known as moments and, occasionally, torque.
torque = moment of force x turning effect
Effects of Force
An object can change its size or shape, begin moving, stop moving, accelerate, or decelerate as a result of a force acting on it. The combined effect of all the forces acting on an object is known as the "resultant force," and it is the same as if only one force were to be operating on the object in that direction. To alter an object's velocity, the resulting force is necessary.
The forces acting on the item are balanced if the resultant force is zero.
The object will remain stationary if the resultant force exerted on it is "zero." In this scenario, the object will go straight ahead at a constant pace.
The object will either accelerate or decelerate if the net force acting on it is not zero.
Force is the push or pull that an item with that mass feels and that results in the change in velocity. Newton is the SI unit of force.
F = m x a
Mass is m and acceleration is a.
A body at rest can be forced to move. It can either slow down or stop a moving body. It can quicken the pace of a moving object, and can alter the direction of a moving body as well.
Moment of a Force
An object may pivot about a point due to a force.
The moment of the force is the term used to describe a force's turning effect.
Moments can move clockwise or counterclockwise around a pivot.
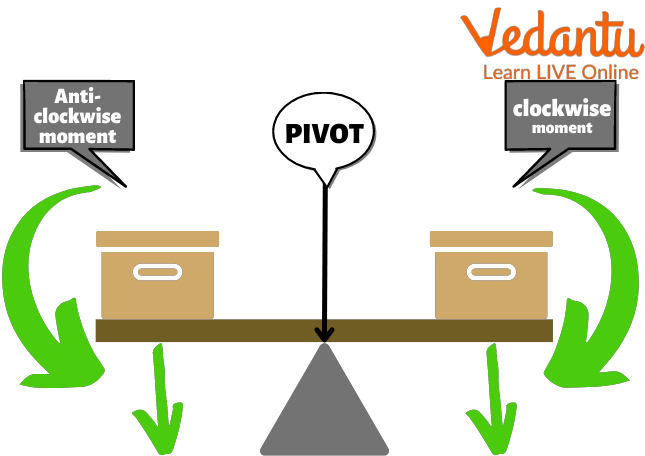
Moment of a Force
The anticlockwise moment acts downward on the left, and the clockwise moment acts downwards on the right.
Calculating the Moment of a Force
The size of the moment of a force can be calculated using the equation:
moment of a force = force (F) x perpendicular distance from the pivot (d)
moment = F x d
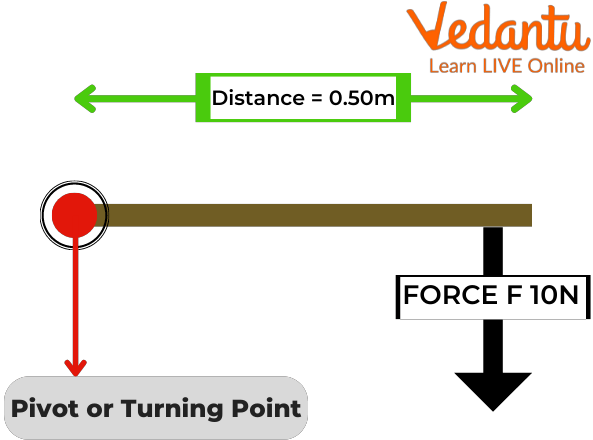
Calculation of Moment of Force
Perpendicular distance from pivot to force d = 0.50 m.
Force F = 10 N
Moment = Fd
Moment = 10 N x 0.50 m
Moment = 5 Nm
This is a clockwise moment.
What is Turning Effect of a Force?
The term "moment of force" or "torque" refers to the action of a force on a rigid body that causes it to rotate around a point, or fulcrum. It is calculated by multiplying the force by the pivot's perpendicular distance from the direction of the force. Newton-metre is its SI equivalent (Nm).
Factors Affecting Turning Effect of Forces
The turning effects of the force depend on a number of variables. These elements are listed below:
The magnitude of applied force.
The applied force and the moment of force are directly proportional.
The perpendicular distance from the pivoted end.
The moment of force is significantly influenced by the angle of perpendicularity between the applied force and the pivot point. It is challenging to generate a big moment of force if the distance between the applied force and the pivot point is less.
For example: A door handle is subjected to a 15 N force at a distance of 12 cm from the hinge. Calculate the moment of force or turning effect of force
Sol: Perpendicular distance from pivot to force d = 12 cm = 0.12 m.
Turning force F = 15 N.
Moment = Fd.
Moment = 15 N x 0.12 m.
Moment = 1.8 Nm.
Summary
This article has shown us that using force in daily life is fairly common. In order to move a given body at a specific speed or direction, lift objects, throw a cricket ball, or walk on a road, we employ force. The many consequences of force are all quite well known to us. We are able to push and pull. Once you understand the underlying concepts, the turning effect of force is not a difficult subject to study! The remaining steps essentially consist of reading the question attentively and making the relevant calculations. We hope you enjoyed reading this article, in case of any other doubts, feel free to ask in the comments.
FAQs on Turning Forces Explained: Physics Made Simple
1. What is the turning effect of a force in Physics?
The turning effect of a force, formally known as the moment of a force or torque, is the tendency of a force to cause or change the rotational motion of an object. When a force is applied to an object that is free to rotate around a fixed point (called a pivot or fulcrum), it produces a turning effect. A classic example is pushing a door open; the force you apply to the handle causes the door to rotate around its hinges.
2. How do you calculate the turning effect of a force (torque)?
The magnitude of the turning effect, or torque (τ), is calculated by multiplying the magnitude of the applied force (F) by the perpendicular distance (r) from the pivot to the line of action of the force. The formula is: τ = F × r. The direction of the moment is either clockwise or anticlockwise, depending on the direction of rotation it would cause.
3. What is the SI unit for the moment of a force?
The SI unit for the moment of a force (torque) is the Newton-metre (N m). This unit is derived directly from its formula, where force is measured in Newtons (N) and the perpendicular distance is measured in metres (m). It is important not to confuse this with Joules (J), which is also N m but represents work or energy.
4. What are some real-world examples of turning forces in action?
The turning effect of forces is a fundamental principle seen in many everyday activities and simple machines. Some common examples include:
Using a spanner to tighten or loosen a nut.
Pushing a door open or closed by its handle.
Pedalling a bicycle, where the force on the pedal creates torque to turn the crank.
Children balancing on a see-saw at a park.
Turning a steering wheel to change a car's direction.
5. What factors determine the magnitude of the turning effect produced by a force?
Two primary factors determine the magnitude of the turning effect (torque):
The magnitude of the force applied: A larger force will produce a greater turning effect, assuming the distance from the pivot is the same.
The perpendicular distance from the pivot: Applying the same force at a greater distance from the pivot will result in a larger turning effect. This is why door handles are placed far from the hinges and long spanners make it easier to turn tight nuts.
6. How does the principle of moments apply to a balanced see-saw?
The principle of moments states that for an object to be in rotational equilibrium (i.e., balanced and not turning), the sum of the clockwise moments about a pivot must be equal to the sum of the anticlockwise moments about the same pivot. On a balanced see-saw, the turning effect created by a person on one side (e.g., clockwise) is perfectly cancelled out by the turning effect created by the person on the other side (anticlockwise).
7. Are 'moment of force' and 'torque' the exact same thing?
In many contexts, especially in introductory physics as per the CBSE syllabus, 'moment of force' and 'torque' are used interchangeably to describe the turning effect of a single force. Both are calculated as force multiplied by perpendicular distance. However, in more advanced physics, 'torque' can specifically refer to the turning effect produced by a couple—a pair of equal and opposite forces that do not act along the same line.
8. What is a 'couple' in the context of turning forces?
A couple consists of two equal, parallel, and oppositely directed forces that do not act along the same line. A couple produces a purely rotational motion without causing any linear motion (translation). For example, when you turn a steering wheel with both hands, your hands apply a couple. Similarly, turning a tap or winding a key involves applying a couple, resulting in pure rotation.

























