
Force on current carrying loop (Radius=R) in uniform magnetic (B) field which is at an angle $30{}^\circ $ with the normal will be
A. Zero
B. $2\pi RiB$
C. $2\sqrt{3}\pi iB$
D. $\pi iB$
Answer
521.1k+ views
Hint: We have a current carrying loop of radius R in a uniform magnetic field. The angle between the normal and the magnetic field is given to us. We know that a current carrying loop will only experience a torque in a uniform magnetic field.
Complete step by step answer:
In the question we are given a current carrying loop of radius R in a uniform magnetic field. The strength of the magnetic field is given as B. the angle between the field and the normal is given as $30{}^\circ $.
The figure below shows a current carrying loop as said in the question.
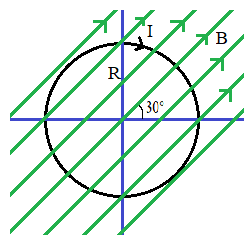
Here we have a uniform magnetic field and a current carrying loop.
We know that a current carrying loop in a uniform magnetic field will only experience torque, i.e. it will not have any force.
Therefore we can say that a current carrying loop in a uniform magnetic field will have a force which is equal to zero.
$\therefore Force=0$
Hence the correct answer is option A.
Note:
As said before, a current carrying loop in a uniform magnetic field will experience a torque.
The equation for torque on a current carrying loop in uniform magnetic field is given as,
$\tau =\vec{\mu }\times \vec{B}$, were ‘$\mu $’ is the magnetic moment and ‘B’ is the magnetic field.
$\Rightarrow \tau =\vec{\mu }\vec{B}\sin \theta $
Magnetic moment can be found using the equation,
$\mu =IA$, were ‘I’ is the current and ‘A’ is the area.
Since ‘R’ is the radius of the loop, we will get the area of the loop as,
$A=\pi {{R}^{2}}$
Therefore we get the magnetic moment as,
$\therefore \mu =\pi {{R}^{2}}I$
Therefore, by substituting this, the equation for torque will become,
$\therefore \tau =\left( \pi {{R}^{2}}I \right)\vec{B}\sin \theta $
From the question we have $\theta =30{}^\circ $
$\therefore \tau =\left( \pi {{R}^{2}}I \right)\vec{B}\sin 30$
$\Rightarrow \tau =\left( \pi {{R}^{2}}I \right)\vec{B}\times \dfrac{1}{2}$
$\therefore \tau =\dfrac{\pi }{2}\vec{B}{{R}^{2}}I$
This is the equation for torque of a current carrying loop in a uniform magnetic field.
Complete step by step answer:
In the question we are given a current carrying loop of radius R in a uniform magnetic field. The strength of the magnetic field is given as B. the angle between the field and the normal is given as $30{}^\circ $.
The figure below shows a current carrying loop as said in the question.

Here we have a uniform magnetic field and a current carrying loop.
We know that a current carrying loop in a uniform magnetic field will only experience torque, i.e. it will not have any force.
Therefore we can say that a current carrying loop in a uniform magnetic field will have a force which is equal to zero.
$\therefore Force=0$
Hence the correct answer is option A.
Note:
As said before, a current carrying loop in a uniform magnetic field will experience a torque.
The equation for torque on a current carrying loop in uniform magnetic field is given as,
$\tau =\vec{\mu }\times \vec{B}$, were ‘$\mu $’ is the magnetic moment and ‘B’ is the magnetic field.
$\Rightarrow \tau =\vec{\mu }\vec{B}\sin \theta $
Magnetic moment can be found using the equation,
$\mu =IA$, were ‘I’ is the current and ‘A’ is the area.
Since ‘R’ is the radius of the loop, we will get the area of the loop as,
$A=\pi {{R}^{2}}$
Therefore we get the magnetic moment as,
$\therefore \mu =\pi {{R}^{2}}I$
Therefore, by substituting this, the equation for torque will become,
$\therefore \tau =\left( \pi {{R}^{2}}I \right)\vec{B}\sin \theta $
From the question we have $\theta =30{}^\circ $
$\therefore \tau =\left( \pi {{R}^{2}}I \right)\vec{B}\sin 30$
$\Rightarrow \tau =\left( \pi {{R}^{2}}I \right)\vec{B}\times \dfrac{1}{2}$
$\therefore \tau =\dfrac{\pi }{2}\vec{B}{{R}^{2}}I$
This is the equation for torque of a current carrying loop in a uniform magnetic field.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

What is transplantation in agriculture class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Who discovered the cell and how class 12 biology CBSE

What is the Full Form of PVC, PET, HDPE, LDPE, PP and PS ?




