
The energy levels of an atom of a certain element are shown in the figure given below. Which of the following transitions A, B, C, D or E will result in the emission of photons of electromagnetic radiation of 618.75 nm? Support your answer with mathematical calculations.

Answer
534.3k+ views
Hint: When the transition of an atom from an upper level to a lower level occurs, energy will be released in the form of photons. The energy of the emitted photons will be equal to the energy difference between the two levels.
Formula Used:
1) The difference in energy between two levels is given by, $\Delta E = {E_1} - {E_2}$ where ${E_1}$ is the energy of that level from which the atom transfers and ${E_2}$ is the energy of that level to which the atom gets transferred.
2) The energy radiation of the emitted photon is given by, $E = \dfrac{{hc}}{\lambda }$ where, $h$ is the Planck's constant, $c$ is the speed of light in vacuum and $\lambda $ is the wavelength of the emitted photon.
Complete step by step answer:
Step 1: Sketch the energy level diagram and list the energy transitions.
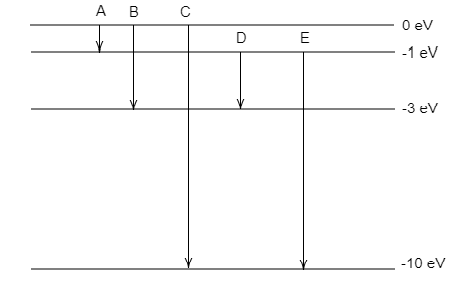
The figure represents five transitions A, B, C, D and E.
Transition A is from 0 eV to −1 eV.
Transition B is from 0 eV to −3 eV.
Transition C is from 0 eV to −10 eV.
Transition D is from −1 eV to −3 eV.
Transition E is from −1 eV to −10 eV.
Each transition will emit photons having energy equal to the corresponding energy difference between the levels.
Step 2: Calculate the energy radiated by the emitted photon.
The wavelength of the energy radiated of the photon is $\lambda = 618.75{\text{nm}}$ .
The energy of the emitted photon is given by, $E = \dfrac{{hc}}{\lambda }$ --------- (1)
where $h$ is the Planck's constant, $c$ is the speed of light in vacuum and $\lambda $ is the wavelength of the emitted photon.
Substituting the values for $h = 6.6 \times {10^{ - 34}}{\text{Js}}$ , $c = 3 \times {10^8}{\text{m/s}}$ and $\lambda = 618.75{\text{nm}}$ in equation (1) we get, $E = \dfrac{{6.626 \times {{10}^{ - 34}} \times 3 \times {{10}^8}}}{{618.75 \times {{10}^{ - 9}}}} = 3.21 \times {10^{ - 19}}{\text{J}}$
We know that, $1{\text{eV = 1}}{\text{.6}} \times {\text{1}}{{\text{0}}^{ - 19}}{\text{J}}$, then in terms of electron Volt, $E = \dfrac{{3.21 \times {{10}^{ - 19}}}}{{1.6 \times {{10}^{ - 19}}}} \cong 2eV$
∴ the energy of the emitted photon is 2eV.
Step 3: From the figure, find the energy transition corresponding to the energy of the emitted photon.
The difference in energy between two levels is given by, $\Delta E = {E_1} - {E_2}$ where ${E_1}$ is the energy of that level from which the atom transfers and ${E_2}$ is the energy of that level to which the atom gets transferred.
From the figure, we can observe that transition D has an energy difference, $\Delta E = - 1 - \left( { - 3} \right) = 2{\text{eV}}$ .
Since the transition energy of D is equal to the energy of the emitted photon, we can conclude that transition D is the required transition.
Note: When substituting values of given physical quantities in an equation, make sure that they are expressed in their respective S.I. units. Necessary conversions must be taken if this is not the case. Atoms transfer from lower levels to upper levels on acquiring energy and transfer from an upper level to a lower level by releasing energy in the form of photons. Here, a transition from the upper level to the lower level took place.
Formula Used:
1) The difference in energy between two levels is given by, $\Delta E = {E_1} - {E_2}$ where ${E_1}$ is the energy of that level from which the atom transfers and ${E_2}$ is the energy of that level to which the atom gets transferred.
2) The energy radiation of the emitted photon is given by, $E = \dfrac{{hc}}{\lambda }$ where, $h$ is the Planck's constant, $c$ is the speed of light in vacuum and $\lambda $ is the wavelength of the emitted photon.
Complete step by step answer:
Step 1: Sketch the energy level diagram and list the energy transitions.

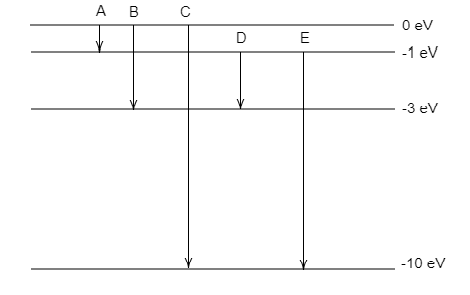
The figure represents five transitions A, B, C, D and E.
Transition A is from 0 eV to −1 eV.
Transition B is from 0 eV to −3 eV.
Transition C is from 0 eV to −10 eV.
Transition D is from −1 eV to −3 eV.
Transition E is from −1 eV to −10 eV.
Each transition will emit photons having energy equal to the corresponding energy difference between the levels.
Step 2: Calculate the energy radiated by the emitted photon.
The wavelength of the energy radiated of the photon is $\lambda = 618.75{\text{nm}}$ .
The energy of the emitted photon is given by, $E = \dfrac{{hc}}{\lambda }$ --------- (1)
where $h$ is the Planck's constant, $c$ is the speed of light in vacuum and $\lambda $ is the wavelength of the emitted photon.
Substituting the values for $h = 6.6 \times {10^{ - 34}}{\text{Js}}$ , $c = 3 \times {10^8}{\text{m/s}}$ and $\lambda = 618.75{\text{nm}}$ in equation (1) we get, $E = \dfrac{{6.626 \times {{10}^{ - 34}} \times 3 \times {{10}^8}}}{{618.75 \times {{10}^{ - 9}}}} = 3.21 \times {10^{ - 19}}{\text{J}}$
We know that, $1{\text{eV = 1}}{\text{.6}} \times {\text{1}}{{\text{0}}^{ - 19}}{\text{J}}$, then in terms of electron Volt, $E = \dfrac{{3.21 \times {{10}^{ - 19}}}}{{1.6 \times {{10}^{ - 19}}}} \cong 2eV$
∴ the energy of the emitted photon is 2eV.
Step 3: From the figure, find the energy transition corresponding to the energy of the emitted photon.
The difference in energy between two levels is given by, $\Delta E = {E_1} - {E_2}$ where ${E_1}$ is the energy of that level from which the atom transfers and ${E_2}$ is the energy of that level to which the atom gets transferred.
From the figure, we can observe that transition D has an energy difference, $\Delta E = - 1 - \left( { - 3} \right) = 2{\text{eV}}$ .
Since the transition energy of D is equal to the energy of the emitted photon, we can conclude that transition D is the required transition.
Note: When substituting values of given physical quantities in an equation, make sure that they are expressed in their respective S.I. units. Necessary conversions must be taken if this is not the case. Atoms transfer from lower levels to upper levels on acquiring energy and transfer from an upper level to a lower level by releasing energy in the form of photons. Here, a transition from the upper level to the lower level took place.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

What is transplantation in agriculture class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Who discovered the cell and how class 12 biology CBSE

What is the Full Form of PVC, PET, HDPE, LDPE, PP and PS ?




