Experiment For Class 9 Physics Force And Pressure Applied On A Cuboid

Pressure is the term used to describe the physical force exerted on an object. It can be described as the proportion of the force to the area across which it is acting.

\[pressure{\rm{ = }}\dfrac{{Force}}{{Area}}\] \[ = \dfrac{F}{A}\]

The fundamental unit of pressure is the Pascal (Pa).

\[1{\rm{ }}pascal{\rm{ }} = {\rm{ }}\dfrac{{1{\rm{ }}Newton}}{{1{\rm{ }}metre{\rm{ }}square}}\]

1 Pa=1 N/m2     

Example: Hammering a sharp pin is simpler than hammering a dull pin. This is because a sharp pin's end has a lower surface area than a blunt pin. This causes the pressure to rise, making it simpler to hit the sharp pin.

The normal force acting on a surface is termed as thrust. Its SI unit is Newton (N).

$Thrust=Pressure\times area$

Example of Thrust: 

An object will lose some weight when submerged in a liquid. This occurs due to the liquid pushing up against the item, which reduces the overall downward force. 

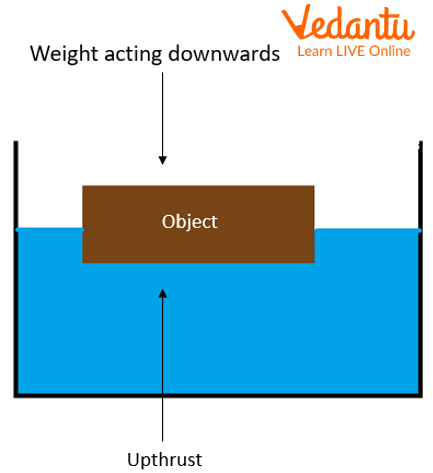
Example of Thrust

Table of content

• Aim

• Theory

• Observation and calculations

• Results

Aim

To observe and compare the pressure a solid iron cuboid would apply to fine sand or wheat flour while resting on each of its three faces and to determine how much pressure would be applied in each situation.

Apparatus Required

• A sturdy iron cuboid with the following components

• A tray with fine sand or beach sand (Tray: 10 x 20 x 30 cm)

• A clamp stand

• Sting 

• Spring balance.

Theory 

• Thrust: The total force a body applies in one direction. (Thrust = bodyweight)

• With respect to the surface, the force is perpendicular. The push acting on the surface is the same if you are standing on loose sand or lying down on it, however, the results are different. As the area of contact shrinks, pressure rises.

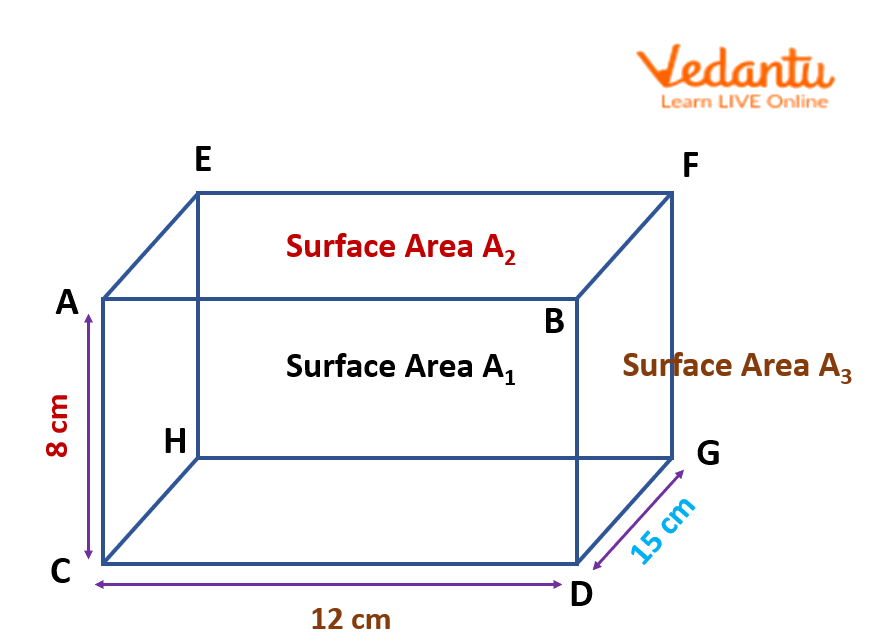
Cuboid

From  this cuboid,  

Surface Area of ABCD, A1

\[\begin{array}{l}{\rm{Area of ABCD  =  Length}} \times {\rm{breadth}}\\{\rm{                          =  12 cm}} \times 8{\rm{ cm}}\\{\rm{                          =  96 c}}{{\rm{m}}^2}\end{array}\]

Surface Area of BDGF, A3

\[\begin{array}{l}{\rm{Area of BDGF  =  15 cm}} \times 8{\rm{ cm}}\\{\rm{                         =  120 c}}{{\rm{m}}^2}\end{array}\]

Surface Area of ABFE, A2

\[\begin{array}{l}{\rm{Area of ABFE  =  15 cm}} \times {\rm{12 cm}}\\{\rm{                         =  180 c}}{{\rm{m}}^2}\end{array}\]

Apparatus Required

A sturdy iron cuboid with the following components: a tray with fine sand or beach sand (Tray: \[15cm \times 25cm \times 30cm\]), a clamp stand, sting and spring balance.

Procedure

1. Procedure of determination of the weight of the given cuboid

1. Attach the cuboid with a string.

2. Make a note of the spring balance's zero deviation.

3. Place the cuboid on the spring balance's hook, which is fastened to the clamp stand.

4. Take note of the spring balance's reading. Record the newton reading on the spring balance if it indicates the cuboid's weight.

If the reading from the spring balance is in g, convert it to newtons as follows:

Change "g" to "kg." Add (g = 9.8 m/s2) to it.

Observation Taken from the Weight of the Given Cuboid

1. From 0 and the first (W0) reading on the spring balance, the number of divisions______________ (n)

2. The spring balance's least accurate reading \[ = {\rm{ }}\dfrac{{{W_0}}}{n}\] =____________

3. reading from a spring balance suspended in air (zero error) = 0

4. Weight of the Cuboid = ____________ N

2. Procedure of determining the pressure applied by different faces of Cuboid

1. First take an empty tray and keep it on the table.

2. Now, fill up the tray with fine sand.

3. Now, place the solid cuboid in the following manner on the tray of fine sand (see the above image of the cuboid for reference):

1. In case (a): The cuboid face with dimensional values of  \[8cm \times 15cm\] should be in touch with the sand  (Surface Area A1)

2. In case (b): The Cuboid face with dimensional values of \[15cm \times 12cm\] should be in touch with the sand (Surface Area A2),

3. In case (c): The cuboid face of the dimensional values of  \[8cm \times 15cm\] should be in touch with the sand  (Surface Area A3),

4. For each case (a, b, and c), keep a close eye on the depressions created by three situations and note down the maximum and minimum depressions brought on by the cuboid using a scale.

5. Now, the values of depressions created by the different faces of the cuboids can be utilised to calculate the pressure created by each dimension—case. i.e., a, b and c

Observations and Calculations Taken from the Pressure Applied by Different Faces of Cuboid

1. In case (a), maximum depression formed in the sand.

2. In case (b), minimum depression formed in the sand.

• Weight of the Cuboid = 1 kg

• Thrust applied on the cuboid,

\[Force = m \times a\]

\[e.g.,1 \times 9.8m/{s^2} = 9.8N\]

• Thrust applied in the Cuboid is the same.

• Surface area,

Case (a):

\[\begin{array}{l}8cm \times 15cm = 120c{m^2}\\{\rm{                   = }}12 \times {10^{ - 3}}{m^2}\end{array}\]

Case (b): 

\[\begin{array}{l}8cm \times 12cm = 96c{m^2}\\{\rm{                   = }}9.6 \times {10^{ - 3}}{m^2}\end{array}\]                 

Case (c): 

\[\begin{array}{l}15cm \times 12cm = 180c{m^2}\\{\rm{                     =  18}} \times {10^{ - 3}}{m^2}\end{array}\]

Observation Table

Results

1. Greater pressure is applied when there is less surface area of contact.

2. Depending on how much of the body's surface area makes contact with the sand, pressure will be applied.

3. The amount of pressure applied by the body directly relates to the depression formed on the sand.

Precautions

1. Place the cuboid on the sand gently.

2. It is important to check the spring balance's proper range and zero error.

3. It is important to acquire exact measurements of the cuboid's weight and the height of the depression in the sand.

4. Sand needs to be moist.

Lab Manual Questions

1. How do area, force, and pressure relate to one another?

Ans: \[pressure{\rm{ = }}\dfrac{{Force}}{{Area}}\]. The amount of pressure applied also rises as force does. The pressure rises as the region shrinks.

2. The spring balance that one should use for an accurate estimate of the cuboid's weight would be of

Ans: Devices with a maximum range and a minimal count produce fewer errors.

3. What distinguishes pressure from force?

Ans: In contrast to pressure, which is the force per unit area, the force applied on an object's surface is equal to its weight.

Viva Questions

1. Explain thrust.

Ans: Thrust is the term for the force that acts on a body perpendicular to its surface.

2. Where on a cuboid does force have the most impact?

Ans: When the cuboid is being kept in an upright position.

3. When does the force's impact become minimal?

Ans: When the cuboid is positioned with its base at its widest.

4. How does the force acting over it affect the contact region?

Ans: Pressure is inversely proportional to the area for forces of the same magnitude. Therefore, the greater the pressure the stronger the force's influence and the smaller the area.

5. Why do knives have a sharp edges, nails have a pointed tips, and buildings have wide foundations?

Ans: The impact of a thrust is dependent on the region on which it acts, according to the fundamental idea of pressure. A smaller pressure is therefore exerted on a wider area by a force of the same magnitude operating on a smaller area, and vice versa. 

6. Why are wooden boards kept underneath railroad tracks?

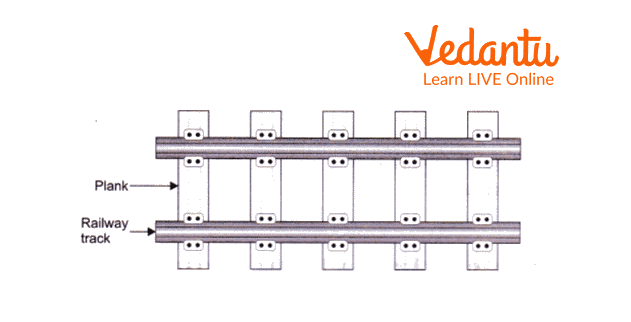
Railroad Tracks

Ans: Trains continuously apply pressure on the railway track, and the planks spread this strain across a larger area to prevent the tracks from sinking into the ground.

7. Does pressure exist in every type of matter?

Ans: Yes, pressure is present in all states of matter—solid, liquid, and gas.

8. How much pressure do you apply on one location of the floor when you swing around on one chair leg as compared to when you sit properly?

Ans: When we sit appropriately, our four legs each experience 4P, or four times as much pressure as the total. However, as it stands currently, the chair's one leg resting on the ground is bearing the entire weight.

9. Why do trucks and buses have considerably broader tyres?

Ans: It is because pressure caused by a truck or bus's weight acting on the road may be small.

10. How will you be arranging relative densities of iron, air, water in increasing order?

Ans: Air, water, iron

Practical Based Questions

1. Pressure is inversely proportional to

1. Length

2. Height

3. Area

4. Volume

Ans: C) Area. Less area means more pressure because pressure is inversely related to area.

2. Pressure can be defined as

1. Mass per unit area

2. Volume per unit area

3. Thrust per unit area

4. Surface per unit area

Ans: C) Thrust per unit area

3. The equipment needed to compare the pressure exerted by a solid iron cuboid is 

1. A tray, a scale, some fine sand, a spring balance, and a string

2. Scale, spring balance, tray, sand, and water.

3. A tray, a spring balance, some coarse sand, and some string.

4. Scale, spring balance, string, tray, and fine wet sand.

Ans: D) Scale, spring balance, string, tray, and fine wet sand.

4. When a cuboid is placed on top of a pointed object that is turned upside down, then the pressure applied on the sand is

1. Increases

2. Decreases

3. Remains same

4. Cannot be determined

Ans: A) Increases

5. A student used two cuboids of the same dimensions and was made of same material to compare the pressure applied by solid iron cuboids. Following the experiment with both cuboids, she discovered

1. p1=p2

2. p1=2p2

3. p1=3p2

4. p2=2p1

Ans: A) p1=p2

6. On top of a layer of sand is a 14 cm x 6 cm x 3 cm iron cuboid. Which one of its surface that come into touch with the sand bed will exert the most pressure?

1. 14 cm × 6 cm

2. 6 cm × 3 cm

3. 14 cm × 3 cm

4. Cannot be determined

Ans: B) 6 cm × 3 cm

7. A student does the experiment by placing the solid iron cuboid on top of some loose sand. Following that, he laid it. These two instances shows that,

1. same thrust but different effects 

2. Both the thrust and its effects are the same.

3. Although there are different thrusts, the results of each are the same.

4. The impact of thrust on sand is less when standing than when laying.

Ans: A) same thrust but different effects

8. When doing the experiment "To examine and compare the pressure applied by solid iron cuboid on sand while resting on its three different faces," the cuboid should be in the which positions? 

1. Base at its widest and upright

2. Wide and side base

3. Side and upright base

4. None of the above

Ans: A) base at its widest and upright

9. The Dam wall’s are broader at the

1. Bottom

2. Top

3. Middle

4. None of the above

Ans: A) Bottom

10. What happens to the air pressure, when there is an increase in altitude

1. Decreases

2. Increases

3. Cannot be determined

4. none of the above

Ans: A) Decreases

Summary

When two objects interact and try to change one another's states, it is called as a force. The force that is delivered perpendicular to an object's surface and spreads across a certain region is known as pressure. From this experiment, we can understand the various pressures exerted on the fine sand in which the positions are being changed. The resultant pressure is therefore stated to be high if the same force is applied to a small area, and it will be low if the same force is applied to a vast area.