Solved NCERT Questions For Class 12 Chemistry Chapter 3 In Hindi - Free PDF
FAQs on NCERT Solutions For Class 12 Chemistry Chapter 3 Electrochemistry Hindi Medium in Hindi - 2025-26
1. Where can I find complete and accurate NCERT Solutions for Class 12 Chemistry Chapter 3, Electrochemistry?
You can find comprehensive, step-by-step NCERT Solutions for all in-text and end-of-chapter exercise questions for Class 12 Chemistry Chapter 3 on Vedantu. These solutions are meticulously prepared by subject matter experts to provide clear methods and are fully aligned with the latest CBSE 2025-26 syllabus and guidelines.
2. What is the correct method to solve the NCERT problem of arranging metals like Al, Cu, Fe, Mg, and Zn based on their displacement power?
The correct method, as explained in the NCERT solutions, relies on the electrochemical series. The steps are as follows:
- Identify the standard reduction potential (E°) for each metal.
- A metal with a more negative E° value is a stronger reducing agent and will displace a metal with a less negative (or positive) E° value from its salt solution.
- Based on their E° values, the correct order in which they displace each other is: Mg > Al > Zn > Fe > Cu.
3. How do the NCERT solutions demonstrate the application of the Nernst equation for calculating cell EMF under non-standard conditions?
The NCERT solutions provide a clear, step-by-step application of the Nernst equation. The method involves:
1. Calculating the standard cell potential (E°cell) from the standard potentials of the anode and cathode.
2. Determining 'n', the number of electrons transferred in the balanced cell reaction.
3. Calculating the reaction quotient, 'Q', using the given molar concentrations of the ionic species.
4. Substituting these values into the Nernst equation (E_cell = E°_cell - (0.0591/n) log Q at 298K) to find the final cell EMF.
4. What is the correct procedure to calculate Gibbs Free Energy (ΔG°) from E°cell in NCERT Chapter 3 problems?
The NCERT solutions for Electrochemistry guide you to use the relationship ΔG° = -nFE°cell. The correct procedure is:
- First, write the balanced cell reaction to determine the value of 'n' (moles of electrons exchanged).
- Next, substitute the values of 'n', the Faraday constant (F ≈ 96500 C mol⁻¹), and the given E°cell into the formula.
- Ensure the final unit is in Joules or Kilojoules per mole as required, remembering that a spontaneous reaction has a positive E°cell and a negative ΔG°.
5. How do the NCERT solutions for Chapter 3 differentiate between solving problems for in-text questions versus end-of-chapter exercises?
The solutions are structured to match the intent of the questions.
- Solutions for in-text questions are typically concise, focusing on the direct application of a specific formula or concept just introduced in the text.
- Solutions for end-of-chapter exercises are more detailed and comprehensive, often requiring the integration of multiple concepts (like linking the Nernst equation with Gibbs energy) and showing a multi-step problem-solving approach.
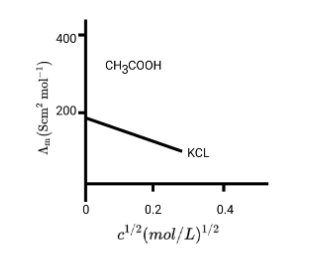
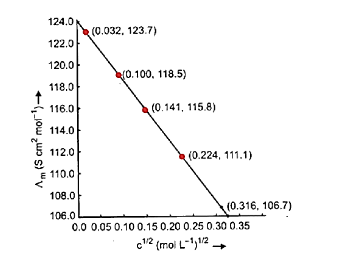
6. What is a common pitfall when solving problems on Kohlrausch's Law for weak electrolytes, and how do the NCERT solutions help avoid it?
A common mistake is attempting to find the limiting molar conductivity (Λ°m) of a weak electrolyte directly. The NCERT solutions clarify that Kohlrausch's Law must be used, which states that Λ°m of an electrolyte is the sum of the individual contributions of its ions. The solutions demonstrate how to algebraically combine the known Λ°m values of strong electrolytes to find the Λ°m of a target weak electrolyte, preventing incorrect direct calculations.
7. Beyond just providing answers, what fundamental relationship between E°cell, ΔG°, and K is clarified by the Chapter 3 NCERT solutions?
The solutions help establish the core connection between these three concepts. They show that a positive E°cell indicates a thermodynamically favourable reaction, which corresponds to a negative Gibbs Free Energy (ΔG°), signifying spontaneity. This, in turn, relates to an Equilibrium Constant (K) greater than 1, meaning the formation of products is favoured. The solutions for numerical problems reinforce how these three values provide a complete picture of a redox reaction's feasibility, spontaneity, and extent.
8. How should one approach solving numericals based on Faraday's laws of electrolysis as per the NCERT solutions?
The NCERT solutions guide a methodical approach. For Faraday's first law, the key is to use the formula W = ZIt, where you first calculate the electrochemical equivalent (Z). For the second law, the solutions show how to use the ratio of masses deposited (W₁/W₂) to the ratio of their equivalent weights (E₁/E₂). The crucial step emphasised is correctly calculating the quantity of charge (Q = I × t) passed and relating it to the moles of substance deposited via the reaction stoichiometry and the Faraday constant.