Question

Discuss the motion of an object under free fall.

Answer 1

Hint: The value of gravitational acceleration as you go up or go down from the Earth’s surface changes. This value changes with height as well as with depth also but for all the phenomena happening close to the Earth’s surface, the gravitational acceleration is almost constant and that constant value is \[g = 9.8\dfrac{m}{{{s^2}}}\] which we also sometimes take as $g = 10\dfrac{m}{{{s^2}}}$ (approx.) for the ease of calculations.

Complete solution:
All objects when dropped from a height, fall towards the Earth’s surface. This happens due to the gravitational force exerted by the Earth on the object. Whenever the object falls to the ground, we can say that the object is in free fall. This happens due to the gravitational force.
The most important thing is that, in free fall, the free falling object accelerates towards the Earth’s surface and this acceleration is because of the gravitational force of the Earth.
Let’s learn it with an example:
When an object moves under the influence of gravity alone, there is no other force which acts on the object then we can say this motion is free fall motion.
If you hold an object at a certain height and release it from there. So we can take the initial velocity of this object as zero and when the object reaches the ground, this object will have the final velocity. Now we will apply this to Newton’s equation of motion $v = u + at$ where $v$ is the final velocity of an object and $u$ is the initial velocity. From this equation, we can write the equation of motion in free fall.

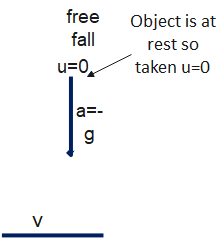
From the above figure, we can say that the initial velocity is zero as the object was at rest initially and we will take $a = g$
So, we can write, $v = gt$ ………..………(i)
Another equation of Newton’s equations of motion is $s = ut + \dfrac{1}{2}a{t^2}$ will become
$s = \dfrac{1}{2}g{t^2}$ …………….………(ii) in free fall
Another equation of motion is ${v^2} = {u^2} + 2as$ so, from the above figure, substitute the value of initial velocity as zero. So, for free fall the equation of motion will be, ${v^2} = 2gs$ …………...…(iii)
In the above equations (i), (ii) & (iii) consider $s$ is the distance travelled, $a$ is acceleration and $g$is acceleration due to gravity and $t$ is time.
So, In this way we can write equations of motion in free fall.
To calculate, the value of $g$, we will use this formula:
$\Rightarrow$ \[g = \dfrac{{G{M_e}}}{{R_e^2}}\]
Where, \[G = 6.67 \times {10^{ - 11}}\dfrac{{N{m^2}}}{{k{g^2}}}\]is known as the universal gravitational constant and ${M_e}$ is the mass of the Earth and ${R_e}$ is the radius of the Earth.
\[\therefore g = \dfrac{{(6.67 \times {{10}^{ - 11}})(6 \times {{10}^{24}})}}{{{{(6.4 \times {{10}^6})}^2}}}\]
$\therefore g = 9.8\dfrac{m}{{{s^2}}}$
Here is an interesting point to learn from the above equation. The interesting point is that the value of $g$does not depend on the size or mass of an object. It depends on the mass of the Earth ${M_e}$ and the radius of the Earth ${R_e}$.

Note: Every object on Earth is attracted towards the center of Earth by Gravity.
The confusion with the sign convention:
Here is the clarification of the sign convention. If we choose downward direction as positive and upward direction as negative direction then,
1. The value of $g$ would be positive if the object is moving in a downward direction.
2. If the object is moving upward, then take $g$ as negative.
If we choose upwards as positive and downwards as negative then $g$ changes accordingly. The value of $g$ depends on the reference frame you select.