
The ratio of its rotational kinetic energy and translational kinetic energy of a sphere, which is rolling without slipping on a horizontal plane, will be:
(A) $5:2$
(B) $2:5$
(C) $7:5$
(D) $5:7$
Answer
180k+ views
Hint The kinetic energy of the body is the sum of its rotational kinetic energy and the translational kinetic energy about the center of mass of the rigid sphere. Here the center of mass is at the point $O$. Also, it has been given that there is no slip, i.e. the relative velocity of the point $A$ on both the sphere and the ground $0$. Therefore we have $v = \omega R$.
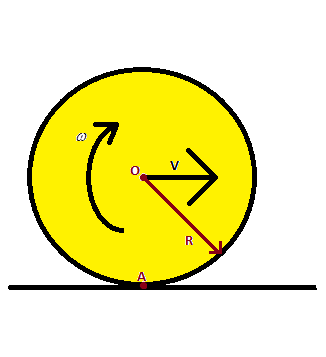
Complete Step by step solution We will separately calculate the rotational kinetic energy and translational kinetic energy and find their ratios. The rotational energy of any body is given by $\dfrac{1}{2}I{\omega ^2}$, where $I$ is the mass moment of inertia, and $\omega $ is the angular velocity about the center of mass of the body $O$.
This energy will vary with different objects as for various objects, the moment of inertia $I$ will vary.
For this solid sphere, $K.E{._{rotational}} = \dfrac{1}{2}I{\omega ^2} = \dfrac{1}{2}(\dfrac{2}{5}M{r^2}){\omega ^2}$
Therefore, substituting $v = \omega R$ in $K.E{._{rotational}} = \dfrac{1}{2}I{\omega ^2} = \dfrac{1}{2}(\dfrac{2}{5}M{r^2}){\omega ^2}$, we get
$ \Rightarrow K.E{._{rotational}} = \dfrac{1}{2}(\dfrac{2}{5}M{r^2}){(\dfrac{v}{r})^2}$,
$ \Rightarrow K.E{._{rotational}} = \dfrac{1}{5}M{v^2}$, where $v$ is the translational velocity at the center of mass of the body $O$.
Now we will find the translational kinetic energy of the solid sphere.
Translational kinetic energy is given by $K.E{._{translational}} = \dfrac{1}{2}M{v^2}$
Now the ratio of the rotational kinetic energy to the translational kinetic energy is, $\dfrac{{K.E{._{rotational}}}}{{K.E{._{translational}}}} = \dfrac{{\dfrac{1}{5}M{v^2}}}{{\dfrac{1}{2}M{v^2}}} = \dfrac{2}{5}$
Hence the correct answer is an option (B).
Note Here we consider the sphere as a solid body. If the sphere would have been hollow, then the moment of inertia would be $\dfrac{{2M{R^2}}}{3}$, in which case the answer would be $\dfrac{{K.E{._{rotational}}}}{{K.E{._{translational}}}} = \dfrac{{\dfrac{1}{3}M{v^2}}}{{\dfrac{1}{2}M{v^2}}} = \dfrac{2}{3}$. The velocity at the contact between the ground and the sphere is $0$ and at the top, most point of the sphere is $v + R\omega $, which is equal to $2v$ , and is the fastest moving point on the sphere.

Complete Step by step solution We will separately calculate the rotational kinetic energy and translational kinetic energy and find their ratios. The rotational energy of any body is given by $\dfrac{1}{2}I{\omega ^2}$, where $I$ is the mass moment of inertia, and $\omega $ is the angular velocity about the center of mass of the body $O$.
This energy will vary with different objects as for various objects, the moment of inertia $I$ will vary.
For this solid sphere, $K.E{._{rotational}} = \dfrac{1}{2}I{\omega ^2} = \dfrac{1}{2}(\dfrac{2}{5}M{r^2}){\omega ^2}$
Therefore, substituting $v = \omega R$ in $K.E{._{rotational}} = \dfrac{1}{2}I{\omega ^2} = \dfrac{1}{2}(\dfrac{2}{5}M{r^2}){\omega ^2}$, we get
$ \Rightarrow K.E{._{rotational}} = \dfrac{1}{2}(\dfrac{2}{5}M{r^2}){(\dfrac{v}{r})^2}$,
$ \Rightarrow K.E{._{rotational}} = \dfrac{1}{5}M{v^2}$, where $v$ is the translational velocity at the center of mass of the body $O$.
Now we will find the translational kinetic energy of the solid sphere.
Translational kinetic energy is given by $K.E{._{translational}} = \dfrac{1}{2}M{v^2}$
Now the ratio of the rotational kinetic energy to the translational kinetic energy is, $\dfrac{{K.E{._{rotational}}}}{{K.E{._{translational}}}} = \dfrac{{\dfrac{1}{5}M{v^2}}}{{\dfrac{1}{2}M{v^2}}} = \dfrac{2}{5}$
Hence the correct answer is an option (B).
Note Here we consider the sphere as a solid body. If the sphere would have been hollow, then the moment of inertia would be $\dfrac{{2M{R^2}}}{3}$, in which case the answer would be $\dfrac{{K.E{._{rotational}}}}{{K.E{._{translational}}}} = \dfrac{{\dfrac{1}{3}M{v^2}}}{{\dfrac{1}{2}M{v^2}}} = \dfrac{2}{3}$. The velocity at the contact between the ground and the sphere is $0$ and at the top, most point of the sphere is $v + R\omega $, which is equal to $2v$ , and is the fastest moving point on the sphere.
Recently Updated Pages
Uniform Acceleration - Definition, Equation, Examples, and FAQs

Difference Between Mass and Weight

JEE Main 2023 April 13 Shift 2 Question Paper with Answer Key

JEE Main 2023 April 11 Shift 2 Question Paper with Answer Key

JEE Main 2023 April 10 Shift 2 Question Paper with Answer Key

JEE Main 2023 (April 8th Shift 2) Physics Question Paper with Answer Key

Trending doubts
Atomic Structure - Electrons, Protons, Neutrons and Atomic Models

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

Degree of Dissociation and Its Formula With Solved Example for JEE

Current Loop as Magnetic Dipole and Its Derivation for JEE

JEE Main Chemistry Question Paper with Answer Keys and Solutions

Find the frictional force between the two blocks in class 11 physics JEE_MAIN

Other Pages
JEE Advanced 2026 Notes

NCERT Solutions For Class 11 Physics Chapter 8 Mechanical Properties Of Solids - 2025-26

The system shown is just on the verge of slipping The class 11 physics JEE_Main

JEE Advanced 2025 Revision Notes for Practical Organic Chemistry

Important Days and Dates in August

MBBS Seats in India 2025: State & College Wise Updates




